Mensuration
- The area of a sector of a circle of radius 5 cm, formed by an arc of length 3.5 cm is:
-
View Hint View Answer Discuss in Forum
Using Rule 17,
Here, l = arc length= 3.5 cm r = radius = 5 cm∴ Area of sector = 1 lr 2 = 1 × 3.5 × 5 = 8.75 cm² 2 Correct Option: B
Using Rule 17,
Here, l = arc length= 3.5 cm r = radius = 5 cm∴ Area of sector = 1 lr 2 = 1 × 3.5 × 5 = 8.75 cm² 2
- The area (in sq. cm.) of the largest circle that can be drawn inside a square of side 28 cm,is :
-
View Hint View Answer Discuss in Forum
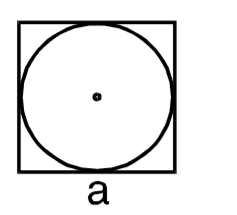
The diameter of the largest circle inscribed inside a square is equal to its side.
∴ d = a = 28cm.Area of the circle = πd² 4 = 1 × 22 × (28)² cm² 4 7
= 22 × 28 cm² = 616 cm²Correct Option: D

The diameter of the largest circle inscribed inside a square is equal to its side.
∴ d = a = 28cm.Area of the circle = πd² 4 = 1 × 22 × (28)² cm² 4 7
= 22 × 28 cm² = 616 cm²
- If the circumference of a circle increases from 4π to 8π, what change occurs in its area?
-
View Hint View Answer Discuss in Forum
When the circumference is doubled, it means radius of circle is doubled, as circumference
= 2πr
Since, area = πr², it will quadrupled.Correct Option: C
When the circumference is doubled, it means radius of circle is doubled, as circumference
= 2πr
Since, area = πr², it will quadrupled.
- The area of the ring between two concentric circles, whose circumference are 88 cm and 132 cm, is :
-
View Hint View Answer Discuss in Forum
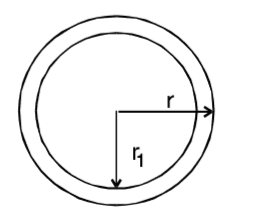
According to question, Circumference of outer circle
= 2πr = 132 cm⇒ r = 132 × 7 = 21 cm 2 × 22
Circumference of inner circle = 2πr1 = 88cm⇒ r1 = 88 × 7 = 14 cm 2 × 22
∴ Area of outer circle = πr²= 22 × 21 × 21 = 1386 cm² 7
and Area of inner circle = πr1²= 22 × 21 × 21 = 1386 cm² 7
∴ Area of ring = (1386 – 616) cm² = 770cm²Correct Option: B

According to question, Circumference of outer circle
= 2πr = 132 cm⇒ r = 132 × 7 = 21 cm 2 × 22
Circumference of inner circle = 2πr1 = 88cm⇒ r1 = 88 × 7 = 14 cm 2 × 22
∴ Area of outer circle = πr²= 22 × 21 × 21 = 1386 cm² 7
and Area of inner circle = πr1²= 22 × 21 × 21 = 1386 cm² 7
∴ Area of ring = (1386 – 616) cm² = 770cm²
- Three circles of radius 3.5 cm each are placed in such a way that each touches the other two. The area of the portion enclosed by the circles is
-
View Hint View Answer Discuss in Forum
Using Rule 6 and 17,
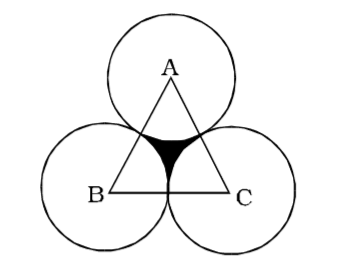
Radius of each circle = 3.5 cm From the figure.
∆ ABC will be an equilateral triangle of side 7 cm each.
Now, the required area = Area of DABC – 3× (Area of a sector of angle 60° in a circle of radius 3.5 cm)= √3 × (7)² - 3 
60 × 22 × (3.5)² 
cm² 4 360 7 = 
49√3 - 19.25 
cm² 4
= [21.217 – 19.25] cm²
= 1.967 cm²Correct Option: B
Using Rule 6 and 17,

Radius of each circle = 3.5 cm From the figure.
∆ ABC will be an equilateral triangle of side 7 cm each.
Now, the required area = Area of DABC – 3× (Area of a sector of angle 60° in a circle of radius 3.5 cm)= √3 × (7)² - 3 
60 × 22 × (3.5)² 
cm² 4 360 7 = 
49√3 - 19.25 
cm² 4
= [21.217 – 19.25] cm²
= 1.967 cm²

