Mensuration
- If the area of a rectangle be (x2 + 7x + 10) sq. cm, then one of the possible perimeter of it is
-
View Hint View Answer Discuss in Forum
x² + 7x + 10
= x² + 5x + 2x + 10
= x (x + 5) + 2 (x + 5) = (x + 2) (x + 5)
∴ Possible perimeter = 2 (x + 2 + x + 5)
= 2 (2x + 7) = (4x + 14) cmCorrect Option: A
x² + 7x + 10
= x² + 5x + 2x + 10
= x (x + 5) + 2 (x + 5) = (x + 2) (x + 5)
∴ Possible perimeter = 2 (x + 2 + x + 5)
= 2 (2x + 7) = (4x + 14) cm
- The perimeter of a rectangular plot is 48 m and area is 108 m². The dimensions of the plot are
-
View Hint View Answer Discuss in Forum
Using Rule 9, If the length and breadth of the plot be x and y respectively, then 2(x + y) = 48
⇒ x + y = 24 .....(i)
xy = 108 .....(ii)
∴ (x – y)² = (x + y)² – 4xy
= (24)² – 4 × 108
= 576 – 432 = 144
∴ x – y = 12 .....(iii)
From equations (i) and (iii),
x = 18 metre and y = 6 metreCorrect Option: D
Using Rule 9, If the length and breadth of the plot be x and y respectively, then 2(x + y) = 48
⇒ x + y = 24 .....(i)
xy = 108 .....(ii)
∴ (x – y)² = (x + y)² – 4xy
= (24)² – 4 × 108
= 576 – 432 = 144
∴ x – y = 12 .....(iii)
From equations (i) and (iii),
x = 18 metre and y = 6 metre
- The sides of a triangle are in the ratio 1/2 : 1/3 : 1/4 . If the perimeter of the triangle is 52 cm, the length of the smallest side is :
-
View Hint View Answer Discuss in Forum
According to question, Ratio of sides of triangle
= 1 : 1 : 1 = 6 : 4 : 3 2 3 4
Now, 6x + 4x + 3x = 52 cm.
13x = 52
∴ x = 4cm
∴ Length of smallest side = 3x = 4 × 3 = 12cmCorrect Option: C
According to question, Ratio of sides of triangle
= 1 : 1 : 1 = 6 : 4 : 3 2 3 4
Now, 6x + 4x + 3x = 52 cm.
13x = 52
∴ x = 4cm
∴ Length of smallest side = 3x = 4 × 3 = 12cm
- The area of an equilateral triangle is 400√3 sq.m. Its perimeter is :
-
View Hint View Answer Discuss in Forum
Using Rule 6, Area of equilateral triangle
= √3 × (side)² 4 = √3 × (side)² = 400√3 4 ⇒(side)² = 400√3 × 4 √3
⇒ Side = √4 × 400 = 40 metres
∴ Perimeter = 3 × side = 3 × 40 = 120 metresCorrect Option: A
Using Rule 6, Area of equilateral triangle
= √3 × (side)² 4 = √3 × (side)² = 400√3 4 ⇒(side)² = 400√3 × 4 √3
⇒ Side = √4 × 400 = 40 metres
∴ Perimeter = 3 × side = 3 × 40 = 120 metres
- From a point in the interior of an equilateral triangle, the perpendicular distance of the sides are √3cm, 2√3cm and 5√3 cm. The perimeter (in cm) of the triangle is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
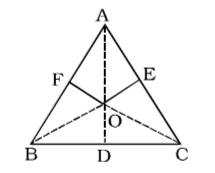
Let ABC be an equilateral triangle of side x cm.
Also, Let OD = √3 cm,
OE = 2√3 cm and OF = 5√3 cm.
From the figure, ar. ∆BOC + ar. ∆AOC + ar. ∆AOB = ar. ∆ABCor, 1 × x × √3 + 1 x × 2√3 + 1 × x ×5√3 = √3 x² 2 2 2 4
or, 2√3 + 4√3 + 10√3 = √3x
or, x = 2 + 4 + 10 = 16
∴ Perimeter of the triangle = 3x = 3 × 16 = 48 cmCorrect Option: C
Using Rule 1,

Let ABC be an equilateral triangle of side x cm.
Also, Let OD = √3 cm,
OE = 2√3 cm and OF = 5√3 cm.
From the figure, ar. ∆BOC + ar. ∆AOC + ar. ∆AOB = ar. ∆ABCor, 1 × x × √3 + 1 x × 2√3 + 1 × x ×5√3 = √3 x² 2 2 2 4
or, 2√3 + 4√3 + 10√3 = √3x
or, x = 2 + 4 + 10 = 16
∴ Perimeter of the triangle = 3x = 3 × 16 = 48 cm

