291. The diameter of the base of a right circular cone is 4 cm and its height 2√3cm. The slant height of the cone is
     

1. 1. 5 cm
      

   
   
   

   2. 4 cm
      

   
   
   

   3. 2√3 cm
      

   
   
   

   4. 3 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Slant height of cone (l ) = √r² + h²
   = √2² + (2√3)²
   = √4 + 12 = √16
   = 4 cm

   Correct Option: B

   Slant height of cone (l ) = √r² + h²
   = √2² + (2√3)²
   = √4 + 12 = √16
   = 4 cm

---

292. The measure of each of two opposite angles of a rhombus is 60° and the measure of one of its sides is 10cm. The length of its smaller diagonal is :
     

1. 1. 10 cm
      

   
   
   

   2. 10√3 cm

   
   
   

   3. 10√2 cm

   
   
   

   4. 5	√2
      2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
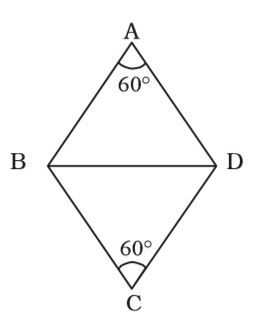
   Let AB = BC = CD = DA = 10 cm
   ∠BAD = ∠BCD = 60°
   ∴ ∠ABC = ∠ADC = 120°
   and ∠CBD = ∠CDB = 60°
   ∴ BD = 10cm

   Correct Option: A

   
   Let AB = BC = CD = DA = 10 cm
   ∠BAD = ∠BCD = 60°
   ∴ ∠ABC = ∠ADC = 120°
   and ∠CBD = ∠CDB = 60°
   ∴ BD = 10cm

---

---

293. A right circular cone is 3.6 cm high and radius of its base is 1.6 cm. It is melted and recast into a right circular cone with radius of its base as 1.2 cm. Then the height of the cone (in cm) is
     

1. 1. 3.6
      

   
   
   

   2. 4.8
      

   
   
   

   3. 6.4
      

   
   
   

   4. 7.2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Volume of cone =	1	πr²h
   	3

   
   

   =	π	× 1.6 × 1.6 × 3.6
   	3

   
   = ⇒ × 1.6 × 1.6 × 1.2 cu.cm.
   

   ∴	1	× 1.2 × 1.2 × H
   	3

   
   (H is height of new cone)
   = π × 1.6 × 1.6 × 1.2
   

   ⇒ H =	1.6 × 1.6 × 3	= 6.4 cm
   	1.2

   Correct Option: C

   Volume of cone =	1	πr²h
   	3

   
   

   =	π	× 1.6 × 1.6 × 3.6
   	3

   
   = ⇒ × 1.6 × 1.6 × 1.2 cu.cm.
   

   ∴	1	× 1.2 × 1.2 × H
   	3

   
   (H is height of new cone)
   = π × 1.6 × 1.6 × 1.2
   

   ⇒ H =	1.6 × 1.6 × 3	= 6.4 cm
   	1.2

---

294. A copper sphere of radius 3 cm is beaten and drawn into a wire of diameter 0.2 cm. The length of the wire is :
     

1. 1. 9 m
      

   
   
   

   2. 12 m
      

   
   
   

   3. 18 m
      

   
   
   

   4. 36 m

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Volume of copper sphere =	4	πr³ =	4	×	22	× 3 × 3 × 3
   	3		3		7

   
   

   =	36 × 22	cm³
   	7

   
   Radius of the wire = 0.1 cm
   The wire can be treated as a solid cylinder.
   Let its length be h cm.
   

   ∴ π × (0.1)² × h =	36 × 22	cm³
   	7

   
   

   ⇒ h = 36 ×	22	×	7	×	1	= 3600 cm = 36 m.
   	7		22		0.01

   
   ∴ Length of the wire = 36 metres.

   Correct Option: D

   Volume of copper sphere =	4	πr³ =	4	×	22	× 3 × 3 × 3
   	3		3		7

   
   

   =	36 × 22	cm³
   	7

   
   Radius of the wire = 0.1 cm
   The wire can be treated as a solid cylinder.
   Let its length be h cm.
   

   ∴ π × (0.1)² × h =	36 × 22	cm³
   	7

   
   

   ⇒ h = 36 ×	22	×	7	×	1	= 3600 cm = 36 m.
   	7		22		0.01

   
   ∴ Length of the wire = 36 metres.

---

---

295. If surface area and volume of a sphere are S and V respectively, then value of S³/V² is
     

1. 1. 36 units
      

   
   
   

   2. 9 units
      

   
   
   

   3. 18 units
      

   
   
   

   4. 27 units

   
   
   

---

1. View Hint View Answer Discuss in Forum

   S = 4πr², V =	4	πr³
   	3

   
   

   ∴	S³		=	64π³r6
   	V²				16	π²r6
   					9

   
   

   =	64π × 9	= 36π
   	16

   Correct Option: A

   S = 4πr², V =	4	πr³
   	3

   
   

   ∴	S³		=	64π³r6
   	V²				16	π²r6
   					9

   
   

   =	64π × 9	= 36π
   	16

---