671. O is the centre of the circle and ∠AOB = 150°, and the shaded portion is x part of the circular region, then x = ?
     
     

1. 1. 1/12
      

   
   
   

   2. 1/9
      

   
   
   

   3. 1/6
      

   
   
   

   4. 1/4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
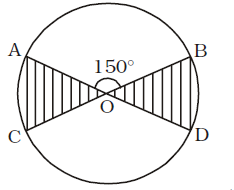
   ∠AOC = ∠BOD = 180° – 150° = 30°
   

   ∴ Area of region x =	60	× πr²
   	360

   
   

   =	1	× πr² sq. cm.
   	6

   Correct Option: C

   
   ∠AOC = ∠BOD = 180° – 150° = 30°
   

   ∴ Area of region x =	60	× πr²
   	360

   
   

   =	1	× πr² sq. cm.
   	6

---

672. The area of the circle with radius y is w. The difference between the areas of the bigger circle (with radius y) and that of the smaller circle (with radius x) is w’. So x/y is equal to
     

1. 1. √1 -	w'
      	w

   
   
   

   2. √1 +	w'
      	w

   
   
   

   3. √1 +	w
      	w'

   
   
   

   4. √1 +	w
      	w'

   
   
   

---

1. View Hint View Answer Discuss in Forum

   w = πy² = Area of larger circle
   w' = πy² – πx²
   ⇒ w' = w – πx²
   ⇒ πx² =
   

   ∴	πx²	=	w – w'
   	πy²		w

   
   

   ⇒	x²	= 1 -	w'
   	y²		w

   
   

   ⇒	x²	= √1 -	w'
   	y²		w

   Correct Option: A

   w = πy² = Area of larger circle
   w' = πy² – πx²
   ⇒ w' = w – πx²
   ⇒ πx² =
   

   ∴	πx²	=	w – w'
   	πy²		w

   
   

   ⇒	x²	= 1 -	w'
   	y²		w

   
   

   ⇒	x²	= √1 -	w'
   	y²		w

---

---

673. D, E and F are the mid points of the sides BC, CA and AB respectively of a ∆ABC. Then the ratio of the areas of ∆DEF and ∆ABC is
     

1. 1. 1/2

   
   
   

   2. 1/4
      

   
   
   

   3. 1/8
      

   
   
   

   4. 1/16

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   EF || CB and FE = 1/2 BC
   ∆DFE ~ ∆ABC
   

   ∴	Area of ∆DEF	=	EF²
   	Area of ∆ABC		BC²

   
   

   =	EF²	=	1
   	4EF²		4

   Correct Option: B

   
   EF || CB and FE = 1/2 BC
   ∆DFE ~ ∆ABC
   

   ∴	Area of ∆DEF	=	EF²
   	Area of ∆ABC		BC²

   
   

   =	EF²	=	1
   	4EF²		4

---

674. An arc AB of a circle subtends an angle x radians at the centre of the circle. Given that the area of the secctor AOB is equal to the square of the length of the arc AB, then the value of x is :
     

1. 1. 1/√2
      

   
   
   

   2. 1/2
      

   
   
   

   3. 1/√3
      

   
   
   

   4. 1/3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
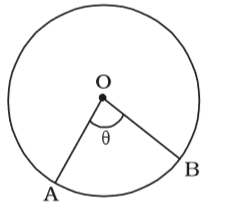
   Let the length of arc AB be y units and radius of circle be r units.
   ∠AOB = x radians
   

   ∴ θ =	l
   	r

   
   

   ⇒ x =	y	......(i)
   	r

   
   Again area of sector AOB
   

   =	θ	× πr² =	x	r² sq units
   	2π		2

   
   According to the question,
   

   xr²	= y² = (xr)² [From equation(i)]
   2

   
   

   ⇒	xr²	= x²r²
   	2

   
   

   ⇒ x =	1
   	2

   
   

   Correct Option: B

   
   Let the length of arc AB be y units and radius of circle be r units.
   ∠AOB = x radians
   

   ∴ θ =	l
   	r

   
   

   ⇒ x =	y	......(i)
   	r

   
   Again area of sector AOB
   

   =	θ	× πr² =	x	r² sq units
   	2π		2

   
   According to the question,
   

   xr²	= y² = (xr)² [From equation(i)]
   2

   
   

   ⇒	xr²	= x²r²
   	2

   
   

   ⇒ x =	1
   	2

---

---

675. The radii of two concentric circles are 68 cm and 22 cm. The area of the closed figure bounded by the boundaries of the circles is
     

1. 1. 4140π sq. cm.
      

   
   
   

   2. 4110π sq. cm.
      

   
   
   

   3. 4080π sq. cm.
      

   
   
   

   4. 4050π sq. cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   R₁ = 68 cm.
   R₂ = 22 cm.
   Area of the shaded region
   = π(R₁² – R₂²)
   = π(R₁ + R₂) (R₁ – R₂)
   = π (68 + 22) (68 – 22)
   = π × 90 × 46 = 4140p sq. cm.

   Correct Option: A

   
   R₁ = 68 cm.
   R₂ = 22 cm.
   Area of the shaded region
   = π(R₁² – R₂²)
   = π(R₁ + R₂) (R₁ – R₂)
   = π (68 + 22) (68 – 22)
   = π × 90 × 46 = 4140p sq. cm.

---