Mensuration
- The areas of a square and a rectangle are equal. The length of the rectangle is greater than the length of any side of the square by 5 cm and the breadth is less by 3 cm. Find the perimeter of the rectangle.
-
View Hint View Answer Discuss in Forum
Using Rule 10,
Let the length of the side of the square be x cm.
∴ x² = (x + 5) (x – 3)
⇒ x² = x² + 5x – 3x – 15⇒ 2x = 15 ⇒ x = 15 cm 2
Now, length of the rectangle= x + 5 = 15 + 5 = 25 cm 2 2
and breadth
== 15 - 3 = 15 - 6 = 9 cm 2 2 2
∴ Required perimeter= 
25 + 9 
= 2 × 34 = 34 cm 2 2 2 Correct Option: D
Using Rule 10,
Let the length of the side of the square be x cm.
∴ x² = (x + 5) (x – 3)
⇒ x² = x² + 5x – 3x – 15⇒ 2x = 15 ⇒ x = 15 cm 2
Now, length of the rectangle= x + 5 = 15 + 5 = 25 cm 2 2
and breadth
== 15 - 3 = 15 - 6 = 9 cm 2 2 2
∴ Required perimeter= 
25 + 9 
= 2 × 34 = 34 cm 2 2 2
- If a wire is bent into the shape of a square, the area of the square is 81 sq. cm. When the wire is bent into a semicircular shape, the area of the semicircle (taking π = 22/7 ) is :
-
View Hint View Answer Discuss in Forum
Using Rule 10,
The length of wire
= perimeter of the square
= 4 × √Area of square
= 4 × √81
= 4 × 9 = 36 cm
Now, perimeter of semicircular shape = 36 cm
⇒ (π × r + 2r) = 36 cm.⇒ r 
22 + 2 
² = 36 cm 7 ⇒ r × 36 = 36 7 ⇒ r × 36 × 7 = 7 cm 7 ∴ Required area = πr² = 22 × 7 × 7 = 77 cm² 2 7 × 2 Correct Option: B
Using Rule 10,
The length of wire
= perimeter of the square
= 4 × √Area of square
= 4 × √81
= 4 × 9 = 36 cm
Now, perimeter of semicircular shape = 36 cm
⇒ (π × r + 2r) = 36 cm.⇒ r 
22 + 2 
² = 36 cm 7 ⇒ r × 36 = 36 7 ⇒ r × 36 × 7 = 7 cm 7 ∴ Required area = πr² = 22 × 7 × 7 = 77 cm² 2 7 × 2
- The perimeter of a rectangle is 160 metre and the difference of two sides is 48 metre. Find the side of a square whose area is equal to the area of this rectangle.
-
View Hint View Answer Discuss in Forum
Let the length and breadth of rectangle are a and b respectively.
According to the question,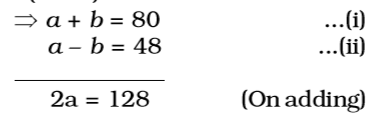
2(a + b) = 160⇒ a = 128 = 64 m 2
From equation (i),
b = 80 – 64 = 16 m
∴ Area of rectangle = 64 × 16 m²
∴ Area of square = 64 × 16 m²
⇒ (side)² = 64 × 16
⇒ side = 8 × 4 = 32 mCorrect Option: A
Let the length and breadth of rectangle are a and b respectively.
According to the question,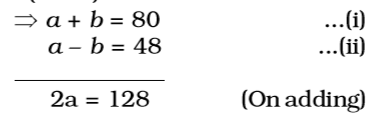
2(a + b) = 160⇒ a = 128 = 64 m 2
From equation (i),
b = 80 – 64 = 16 m
∴ Area of rectangle = 64 × 16 m²
∴ Area of square = 64 × 16 m²
⇒ (side)² = 64 × 16
⇒ side = 8 × 4 = 32 m
- ABC is an equilateral triangle. P and Q are two points on AB and AC respectively such that PQ || BC . If PQ = 5 cm, then area of ∆APQ is :
-
View Hint View Answer Discuss in Forum
Using Rule 6,
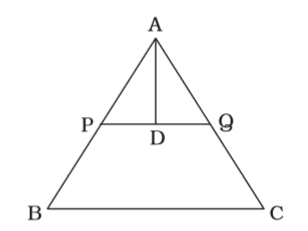
PQ Ω BC
∠APQ = ∠ABC = 60°
∠AQP = ∠ACB = 60°∴ Area of ∆APQ = √3 × (PQ)² 4 = √3 × 5² = 25√3 sq. cm. 4 4 Correct Option: C
Using Rule 6,

PQ Ω BC
∠APQ = ∠ABC = 60°
∠AQP = ∠ACB = 60°∴ Area of ∆APQ = √3 × (PQ)² 4 = √3 × 5² = 25√3 sq. cm. 4 4
- The area (in m2) of the square which has the same perimeter as a rectangle whose length is 48 m and is 3 times its breadth, is :
-
View Hint View Answer Discuss in Forum
Using Rule 9 and 10,
Let the length of rectangle = 48 m. and
breadth = 16m.
Perimeter of square = Perimeter of rectangle = 2(48 + 16)
⇒ 4 × Side = 2 × 64⇒ Side = 2 + 64 = 32 metres 4
⇒ Area of the square = (32)² = 1024 metre²Correct Option: B
Using Rule 9 and 10,
Let the length of rectangle = 48 m. and
breadth = 16m.
Perimeter of square = Perimeter of rectangle = 2(48 + 16)
⇒ 4 × Side = 2 × 64⇒ Side = 2 + 64 = 32 metres 4
⇒ Area of the square = (32)² = 1024 metre²

