Mensuration
- In trapezium ABCD, AB ||CD and AB = 2CD. Its diagonals intersect at O. If the area of ∆AOB = 84 cm², then the area of ∆COD is equal to
-
View Hint View Answer Discuss in Forum
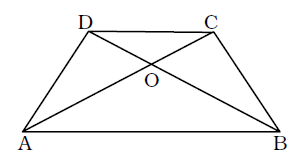
DC || AB
∠DCA = ∠CAB
∠CDB = ∠DBA
∴ ∆COD ~ ∆AOB∴ Area of ∆COD Area of ∆AOB = CD² = CD² = 1 AB² 4CD² 4
∴ Area of ∆COD= 1 × 84 4
= 21 sq. cm.Correct Option: B

DC || AB
∠DCA = ∠CAB
∠CDB = ∠DBA
∴ ∆COD ~ ∆AOB∴ Area of ∆COD Area of ∆AOB = CD² = CD² = 1 AB² 4CD² 4
∴ Area of ∆COD= 1 × 84 4
= 21 sq. cm.
- Given that the ratio of altitudes of two triangles is 4 : 5, ratio of their areas is 3 : 2. The ratio of their corresponding bases is
-
View Hint View Answer Discuss in Forum
Using Rule 1,
Area of triangle = 1 × base × height 2 = 1 × b × h 2 ∴ According to the question, 1 b1h1 2 1 b2h2 4 = 3 2 ⇒ b1 × 4 = 3 b2 5 2 ⇒ b1 = 3 × 5 = 15 = 15 : 8 b2 2 4 8 Correct Option: B
Using Rule 1,
Area of triangle = 1 × base × height 2 = 1 × b × h 2 ∴ According to the question, 1 b1h1 2 1 b2h2 4 = 3 2 ⇒ b1 × 4 = 3 b2 5 2 ⇒ b1 = 3 × 5 = 15 = 15 : 8 b2 2 4 8
- The area of an isosceles trapezium is 176 cm² and the height is
2/11 th of the sum of its parallel sides. If the ratio of the length of the parallel sides is 4 : 7, then the length of a diagonal (in cm) is
-
View Hint View Answer Discuss in Forum
Using Rule 13,
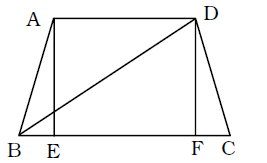
BC = 7x cm.
AD = 4x cm.
AB = DC ;
AE ⊥ BC ; DF ⊥ BC
Area of trapezium ABCD= 1 × (AD + BC) × AE 2 ⇒ 176 = 1 × 11x × 11x × 11x 2 11
⇒ 176 = 11x²⇒ x² = 176 = 16 11
⇒ x = √16 = 4
∴ BC = 7 × 4 = 28 cm.
AD = 4 × 4 = 16 cm.∴ BE = FC = 1 (28 - 16) cm 2
= 6 cm.
∴ BF = 16 + 6 = 22 cm.∴ DF = 2 × 11x = 2x 11
= 8 cm.
∴ Diagonal BD = √BF² + FB²
= √ 22² + 8²
= √484 + 64
= √548 = 4 √4 × 137
= 2√137 cm.Correct Option: C
Using Rule 13,

BC = 7x cm.
AD = 4x cm.
AB = DC ;
AE ⊥ BC ; DF ⊥ BC
Area of trapezium ABCD= 1 × (AD + BC) × AE 2 ⇒ 176 = 1 × 11x × 11x × 11x 2 11
⇒ 176 = 11x²⇒ x² = 176 = 16 11
⇒ x = √16 = 4
∴ BC = 7 × 4 = 28 cm.
AD = 4 × 4 = 16 cm.∴ BE = FC = 1 (28 - 16) cm 2
= 6 cm.
∴ BF = 16 + 6 = 22 cm.∴ DF = 2 × 11x = 2x 11
= 8 cm.
∴ Diagonal BD = √BF² + FB²
= √ 22² + 8²
= √484 + 64
= √548 = 4 √4 × 137
= 2√137 cm.
- The area of a circle whose radius is the diagonal of a square whose area is 4 sq. units is :
-
View Hint View Answer Discuss in Forum
Using Rule 10,
Side of square = √4
= 2 units Diagonal of square = 2√2 units
= radius of the circle
× Area of circle = πr²
= π × (2√2)²
= 8π sq. units.Correct Option: D
Using Rule 10,
Side of square = √4
= 2 units Diagonal of square = 2√2 units
= radius of the circle
× Area of circle = πr²
= π × (2√2)²
= 8π sq. units.
- A rectangular carpet has an area of 120 m² and a perimeter of 46 metre. The length of its diagonal is :
-
View Hint View Answer Discuss in Forum
Using Rule 9,
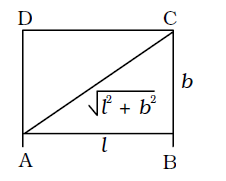
Let the length of carpet be l metre and breadth be b metre.
∴ Diagonal = √l² + b² ...(i)
According to the question, lb = 120
and, 2 (l + b) = 46
⇒ l + b = 23
On squaring both sides, (l + b)² = 23²
⇒ l2 + b² + 2lb = 529
⇒ l2 + b² + 2 × 120 = 529
⇒ l2 + b² = 529 – 240 = 289
⇒ √l² + b² = √289 = 17 metre
= Diagonal of the carpetCorrect Option: C
Using Rule 9,

Let the length of carpet be l metre and breadth be b metre.
∴ Diagonal = √l² + b² ...(i)
According to the question, lb = 120
and, 2 (l + b) = 46
⇒ l + b = 23
On squaring both sides, (l + b)² = 23²
⇒ l2 + b² + 2lb = 529
⇒ l2 + b² + 2 × 120 = 529
⇒ l2 + b² = 529 – 240 = 289
⇒ √l² + b² = √289 = 17 metre
= Diagonal of the carpet

