Mensuration
- By melting two solid metallic spheres of radii 1 cm and 6 cm, a hollow sphere of thickness 1 cm is made. The external radius of the hollow sphere will be
-
View Hint View Answer Discuss in Forum
Volume of two solid metallic spheres = 4 π(r1³ + r2³) 3 = 4π (1³ + 6³) 3 = 4π (1 + 216) 3 = 
4π × 217 
cu.cm. 3
Internal radius of hollow sphere = r cm (let)= 4 π((r + 1)³ + r³) 3 = 4π × 217 3
⇒ r³+ 3r² + 3r + 1 – r³ = 217
⇒ 3r² + 3r + 1 = 217
⇒ 3r² + 3r – 216 = 0
⇒ r² + r – 72 = 0
⇒ r² + 9r – 8r – 72 = 0
⇒ r (r + 9) – 8 (r + 9) = 0
⇒ (r – 8) (r + 9) = 0
⇒ r = 8 cm. because r ≠ –9
∴ External radius of hollow sphere = 9 cmCorrect Option: A
Volume of two solid metallic spheres = 4 π(r1³ + r2³) 3 = 4π (1³ + 6³) 3 = 4π (1 + 216) 3 = 
4π × 217 
cu.cm. 3
Internal radius of hollow sphere = r cm (let)= 4 π((r + 1)³ + r³) 3 = 4π × 217 3
⇒ r³+ 3r² + 3r + 1 – r³ = 217
⇒ 3r² + 3r + 1 = 217
⇒ 3r² + 3r – 216 = 0
⇒ r² + r – 72 = 0
⇒ r² + 9r – 8r – 72 = 0
⇒ r (r + 9) – 8 (r + 9) = 0
⇒ (r – 8) (r + 9) = 0
⇒ r = 8 cm. because r ≠ –9
∴ External radius of hollow sphere = 9 cm
- Height of a prism–shaped part of a machine is 8 cm and its base is an isosceles triangle, whose each of the equal sides is 5 cm and remaining side is 6 cm. The volume of the part is
-
View Hint View Answer Discuss in Forum
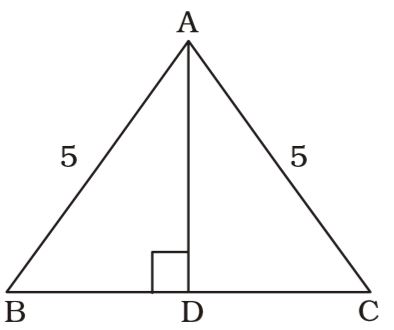
AB = AC = 5 cm.
BD = DC = 3 cm.
From ∆ABD,
AD = √AB² - BD² = √5² - 3² = √25 - 9
= √16 = 4 cm.∴ Area of the base of prism = 1 × BC × AD 2 = 1 × 6 × 4 = 12 sq. cm. 2
∴ Volume of prism = Area of base × height = 12 × 8 = 96 cu. cm.Correct Option: A

AB = AC = 5 cm.
BD = DC = 3 cm.
From ∆ABD,
AD = √AB² - BD² = √5² - 3² = √25 - 9
= √16 = 4 cm.∴ Area of the base of prism = 1 × BC × AD 2 = 1 × 6 × 4 = 12 sq. cm. 2
∴ Volume of prism = Area of base × height = 12 × 8 = 96 cu. cm.
- A cuboidal shaped water tank, 2.1 m long and 1.5 m broad is half filled with water. If 630 litres more water is poured into that tank, the water level will rise
-
View Hint View Answer Discuss in Forum
Increase in water level = x cm (let)
According to the question, 2.1 × 1.5 × 10000 × x = 630 × 1000 cu. cm.
⇒ 21 × 15 × 100 × x = 630000⇒ x = 630000 = 20 cm. = 0.2 metre 21 × 15 × 100 Correct Option: B
Increase in water level = x cm (let)
According to the question, 2.1 × 1.5 × 10000 × x = 630 × 1000 cu. cm.
⇒ 21 × 15 × 100 × x = 630000⇒ x = 630000 = 20 cm. = 0.2 metre 21 × 15 × 100
- A solid sphere of radius 9 cm is melted to form a sphere of radius 6 cm and a right circular cylinder of same radius. The height of the cylinder so formed is
-
View Hint View Answer Discuss in Forum
Volume of larger sphere = 4 πR³ = 4 π(9)³ cu.cm. 3 3
= 972π cu.cm.Volume of smaller sphere = 4 π(6)³ = 288π cu.cm. 3
Volume of cylinder = πr²h
= π × 36h = 36ph cu.cm.
∴ 288π + 36π h = 972π
⇒ 288 + 36h = 972
⇒ 36h = 972 – 288 = 684⇒ h = 684 = 19 cm. 36 Correct Option: A
Volume of larger sphere = 4 πR³ = 4 π(9)³ cu.cm. 3 3
= 972π cu.cm.Volume of smaller sphere = 4 π(6)³ = 288π cu.cm. 3
Volume of cylinder = πr²h
= π × 36h = 36ph cu.cm.
∴ 288π + 36π h = 972π
⇒ 288 + 36h = 972
⇒ 36h = 972 – 288 = 684⇒ h = 684 = 19 cm. 36
- A hollow cylindrical tube 20 cm. long is made of iron and its external and internal diameters are 8 cm. and 6 cm. respectively. The volume (in cubic cm.) of iron used in making the tube is (Use π = 22/7)
-
View Hint View Answer Discuss in Forum
Volume of used iron = π(R² – r²)h
where R = 4 cm; r = 3 cm.= 22 (4² – 3²) × 20 7 = 22 × (4 + 3)(4 – 3) × 20 7 = 22 × 7 × 20 = 440 cu.cm. 7 Correct Option: B
Volume of used iron = π(R² – r²)h
where R = 4 cm; r = 3 cm.= 22 (4² – 3²) × 20 7 = 22 × (4 + 3)(4 – 3) × 20 7 = 22 × 7 × 20 = 440 cu.cm. 7

