Mensuration
- 360 sq. cm and 250 sq. cm are the area of two similar triangles. If the length of one of the sides of the first triangle be 8 cm, then the length of the corresponding side of the second triangle is
-
View Hint View Answer Discuss in Forum
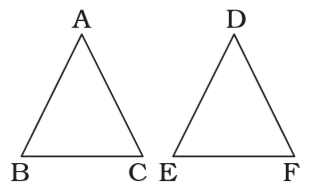
ar(∆ ABC) = AB² ar(∆ DEF) DE² ⇒ 360 = 8 × 8 250 DE² ⇒ DE² = 8 × 8 × 250 = 8² × 5² 360 6² ⇒ DE = 8 × 5 = 20 = 6 2 cm 6 3 3 Correct Option: C

ar(∆ ABC) = AB² ar(∆ DEF) DE² ⇒ 360 = 8 × 8 250 DE² ⇒ DE² = 8 × 8 × 250 = 8² × 5² 360 6² ⇒ DE = 8 × 5 = 20 = 6 2 cm 6 3 3
- The perimeter of an isosceles triangle is 544 cm and each of the equal sides is 5/6 times the base. What is the area (in cm²) of the triangle ?
-
View Hint View Answer Discuss in Forum

Let AD be the altitude.
Base = x cmEach equal side = 5x cm 6 ∴ x + 2 × 5x = 544 6 ⇒ 3x + 5x = 544 3
⇒ 8x = 544 × 3⇒ x = 544 × 3 = 204 8
∴ BD = 102 cm⇒ AB = 5x = 5 × 204 = 170 cm 6 6
and AD = √AB² - BD²
= √170² - 102²
= √(170 + 102)(170 - 102)
= √272 × 68 = 136cm∴ ∆ ABC = 1 BC × AD 2 = 1 × 204 × 136 2
= 13872 sq.cm.Correct Option: D

Let AD be the altitude.
Base = x cmEach equal side = 5x cm 6 ∴ x + 2 × 5x = 544 6 ⇒ 3x + 5x = 544 3
⇒ 8x = 544 × 3⇒ x = 544 × 3 = 204 8
∴ BD = 102 cm⇒ AB = 5x = 5 × 204 = 170 cm 6 6
and AD = √AB² - BD²
= √170² - 102²
= √(170 + 102)(170 - 102)
= √272 × 68 = 136cm∴ ∆ ABC = 1 BC × AD 2 = 1 × 204 × 136 2
= 13872 sq.cm.
- The altitude drawn to the base of an isosceles triangle is 8 cm and its perimeter is 64 cm. The area (in cm²) of the triangle is
-
View Hint View Answer Discuss in Forum
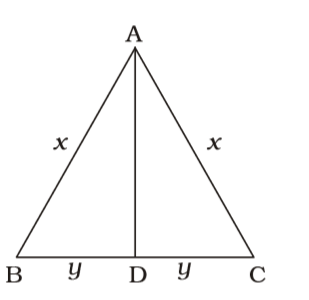
Let AB = AC = x cm
and BD = DC = y cm
then, AD² = x² – y²
⇒ x² – y² = 64
x + x + 2y = 64
⇒ 2x + 2y = 64
⇒ x + y = 32∴ x² - y² = 64 x + y 32 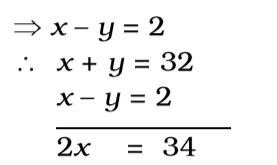
⇒ x = 17 cm
Also, x + y = 32
⇒ y = 32 – 17 = 15 cm∴ area of ∆ ABC = 1 × BC × AD 2 = 1 × 30 × 8 = 120 sq. cm. 2 Correct Option: D

Let AB = AC = x cm
and BD = DC = y cm
then, AD² = x² – y²
⇒ x² – y² = 64
x + x + 2y = 64
⇒ 2x + 2y = 64
⇒ x + y = 32∴ x² - y² = 64 x + y 32 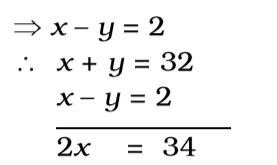
⇒ x = 17 cm
Also, x + y = 32
⇒ y = 32 – 17 = 15 cm∴ area of ∆ ABC = 1 × BC × AD 2 = 1 × 30 × 8 = 120 sq. cm. 2
- The perimeter of a rhombus is 40 m and its height is 5 m. Its area is :
-
View Hint View Answer Discuss in Forum
Using Rule 12,
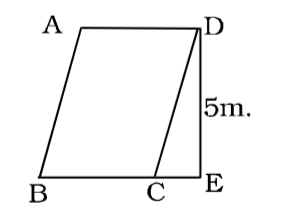
Perimeter of rhombus
= 4 × side
∴ 4 × side = 40⇒ side = 40 = 10m 4
As, rhombus is a parallelogram of equal sides, its area
= base × height = 10 × 5 = 50m².Correct Option: B
Using Rule 12,

Perimeter of rhombus
= 4 × side
∴ 4 × side = 40⇒ side = 40 = 10m 4
As, rhombus is a parallelogram of equal sides, its area
= base × height = 10 × 5 = 50m².
- The area of a field in the shape of a trapezium measures 1440 m². The perpendicular distance between its parallel sides is 24 m. If the ratio of the parallel sides is 5 : 3, the length of the longer parallel side is :
-
View Hint View Answer Discuss in Forum
Using Rule 13,
Let the parallel sides be 5x and 3x metres.
Area of trapezium = 1/2 (sum of parallel sides) × distance between them⇒ 1440 = 1 (5x + 3x) × 24 2
⇒ 12 × 8x = 1440⇒ x = 1440 = 15 12 × 8
∴ The longer parallel side = 5x = 5 × 15 = 75 metresCorrect Option: A
Using Rule 13,
Let the parallel sides be 5x and 3x metres.
Area of trapezium = 1/2 (sum of parallel sides) × distance between them⇒ 1440 = 1 (5x + 3x) × 24 2
⇒ 12 × 8x = 1440⇒ x = 1440 = 15 12 × 8
∴ The longer parallel side = 5x = 5 × 15 = 75 metres

