Mensuration
- A rectangular park 60 metre long and 40 metre wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 metre² then the width of the road is
-
View Hint View Answer Discuss in Forum
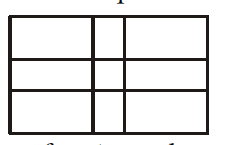
Area of rectangular park = 60 × 40 = 2400 sq. metre
Let the width of cross-road be x metre.
∴ Area of cross-roads = 60x + 40x – x²
= 100x – x²
According to the question,
100x – x² = 2400 – 2109
⇒ 100x – x² = 291
⇒ x² – 100x + 291 = 0
⇒ x² – 3x – 97x + 291 = 0
⇒ x (x – 3) – 97 (x – 3) = 0
⇒ (x – 3) (x – 97) = 0
⇒ x = 3 because x ≠ 97Correct Option: A

Area of rectangular park = 60 × 40 = 2400 sq. metre
Let the width of cross-road be x metre.
∴ Area of cross-roads = 60x + 40x – x²
= 100x – x²
According to the question,
100x – x² = 2400 – 2109
⇒ 100x – x² = 291
⇒ x² – 100x + 291 = 0
⇒ x² – 3x – 97x + 291 = 0
⇒ x (x – 3) – 97 (x – 3) = 0
⇒ (x – 3) (x – 97) = 0
⇒ x = 3 because x ≠ 97
- A square and a regular hexagon are drawn such that all the vertices of the square and the hexagon are on a circle of radius r cm. The ratio of area of the square and the hexagon is
-
View Hint View Answer Discuss in Forum
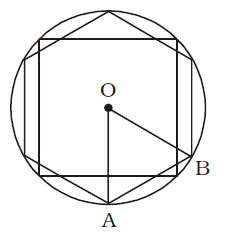
Diagonal of square = 2r cm.∴ Area of square = 1 × (2r)² = 2r² sq.cm. 2 Area of ∆OAB = √3 r² sq.cm. 4 ∴ Area of hexagon = 6√3 r² 4 = 3√3 r² sq.cm. 2 ∴ Required ratio = 2r² : 3√3 r² 2
= 4 : 3√3Correct Option: B

Diagonal of square = 2r cm.∴ Area of square = 1 × (2r)² = 2r² sq.cm. 2 Area of ∆OAB = √3 r² sq.cm. 4 ∴ Area of hexagon = 6√3 r² 4 = 3√3 r² sq.cm. 2 ∴ Required ratio = 2r² : 3√3 r² 2
= 4 : 3√3
- If D and E are the mid-points of AB and AC respectively of ∆ABC, then the ratio of the areas of ∆ADE and B∎ CED is
-
View Hint View Answer Discuss in Forum
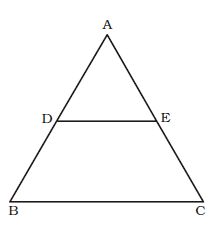
DE || BC and DE = 1 BC 2 ∴ Area of ∆ABC = BC² = 4 Area of ∆ADE DE² ∴ Area of ∆ADE = 1 × Area of ∆ABC 4
Area of ∎ BCED= 3 × Area of ∆ABC 4
∴ Required ratio = 1 : 3Correct Option: D

DE || BC and DE = 1 BC 2 ∴ Area of ∆ABC = BC² = 4 Area of ∆ADE DE² ∴ Area of ∆ADE = 1 × Area of ∆ABC 4
Area of ∎ BCED= 3 × Area of ∆ABC 4
∴ Required ratio = 1 : 3
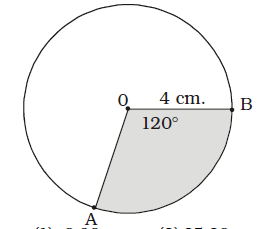
- What is the area of dark (coloured) sector for the figure given below?
-
View Hint View Answer Discuss in Forum

∵ 360° ≡ πr²∴ 120° ≡ 120 × πr² 360 ≡ πr² = 22 × 4 × 4 3 7 × 3 = 352 = 16.76 sq. cm 21 Correct Option: C

∵ 360° ≡ πr²∴ 120° ≡ 120 × πr² 360 ≡ πr² = 22 × 4 × 4 3 7 × 3 = 352 = 16.76 sq. cm 21
- If two medians BE and CF of a triangle ABC, intersect each other at G and if BG = CG, angle BGC = 120°, BC = 10 cm, then area of the triangle ABC is :
-
View Hint View Answer Discuss in Forum

BG = GC, ∠BGC = 120°
∴ ∠GBC = ∠GCB = 30°
∴ ∆ABC is an equilateral triangle.∴ Area of ∆ABC = √3 × side² 4 = √3 × 10 × 10 4
= 25√3 Sq. cm.Correct Option: D

BG = GC, ∠BGC = 120°
∴ ∠GBC = ∠GCB = 30°
∴ ∆ABC is an equilateral triangle.∴ Area of ∆ABC = √3 × side² 4 = √3 × 10 × 10 4
= 25√3 Sq. cm.

