Mensuration
- The ratio of inradius and circumradius of a square is :
-
View Hint View Answer Discuss in Forum
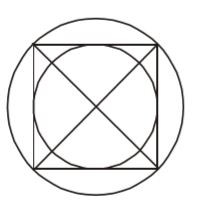
Radius of circum-circle = Diagonal = √2 × Side = Side 2 2 √2 Radius of in-circle = Side 2 ∴ Ratio = Side : Side = 1 : √2 2 √2 Correct Option: A

Radius of circum-circle = Diagonal = √2 × Side = Side 2 2 √2 Radius of in-circle = Side 2 ∴ Ratio = Side : Side = 1 : √2 2 √2
- The perimeter of a rectangle and a square are 160 m each. The area of the rectangle is less than that of the square by 100 sq m. The length of the rectangle is
-
View Hint View Answer Discuss in Forum
Let the length and breadth of rectangle be x and y m. respectively.
According to the question, 2 (x + y) = 160⇒ x + y = 160 = 80 m...........(i) 2
Perimeter of square = 160 m∴ Side of square = 160 = 40 m 4
Now,
Area of rectangle = xy
Area of square = 40 × 40 = 1600 m²
Then,
1600 – xy = 100
⇒ xy = 1600 – 100 = 1500 ..(ii)
Now,
(x – y)² = (x + y)² – 4xy
= (80)² – 4 × 1500
= 6400 – 6000 = 400
⇒ x – y = √400 = 20 ...(iii)
From equations (i) and (iii),
2x = 100⇒ x = 100 = 50 m 2 Correct Option: D
Let the length and breadth of rectangle be x and y m. respectively.
According to the question, 2 (x + y) = 160⇒ x + y = 160 = 80 m...........(i) 2
Perimeter of square = 160 m∴ Side of square = 160 = 40 m 4
Now,
Area of rectangle = xy
Area of square = 40 × 40 = 1600 m²
Then,
1600 – xy = 100
⇒ xy = 1600 – 100 = 1500 ..(ii)
Now,
(x – y)² = (x + y)² – 4xy
= (80)² – 4 × 1500
= 6400 – 6000 = 400
⇒ x – y = √400 = 20 ...(iii)
From equations (i) and (iii),
2x = 100⇒ x = 100 = 50 m 2
- The volume of a right circular cylinder and that of a sphere are equal and their radii are also equal. If the height of the cylinder be h and the diameter of the sphere d, then which of the following relation is correct ?
-
View Hint View Answer Discuss in Forum
Volume of the cylinder = πr²h
= πd²h cubic units 4 
∵ r = d 
2 Volume of sphere = 4 π 
h 
³ 3 2 = π d³ cubic units 6
According to the question,π d³ = πd²h 6 4 ⇒ d = h ⇒ 4d = 6h 6 4
⇒ 2d = 3hCorrect Option: D
Volume of the cylinder = πr²h
= πd²h cubic units 4 
∵ r = d 
2 Volume of sphere = 4 π 
h 
³ 3 2 = π d³ cubic units 6
According to the question,π d³ = πd²h 6 4 ⇒ d = h ⇒ 4d = 6h 6 4
⇒ 2d = 3h
- A solid cone of height 9 cm with diameter of its base 18 cm is cut out from a wooden solid sphere of radius 9 cm. The percentage of wood wasted is :
-
View Hint View Answer Discuss in Forum
Volume of sphere = 4 πr³ 3 = 4 π × 9 × 9 × 9 = 972π cu.cm. 3 Volume of cone = 1 πR²H 3 = 1 π × 9 × 9 × 9 = 243π cu.cm. 3 ∴ Percentage of wood wasted = (972π - 243π) × 100 972π
= 75%
Method 2 :
Quicker Approach
In both cases
∵ r = 9, h = 9cm∴ Volume of sphere = 4 πr³ 3 and Volume of cone = 1 πr³ 3
Wasted wood = πr³∴ Required percentage = πr³ × 100 4 πr³ 3 = 3 × 100 = 75% 4 Correct Option: D
Volume of sphere = 4 πr³ 3 = 4 π × 9 × 9 × 9 = 972π cu.cm. 3 Volume of cone = 1 πR²H 3 = 1 π × 9 × 9 × 9 = 243π cu.cm. 3 ∴ Percentage of wood wasted = (972π - 243π) × 100 972π
= 75%
Method 2 :
Quicker Approach
In both cases
∵ r = 9, h = 9cm∴ Volume of sphere = 4 πr³ 3 and Volume of cone = 1 πr³ 3
Wasted wood = πr³∴ Required percentage = πr³ × 100 4 πr³ 3 = 3 × 100 = 75% 4
- Two circles with centres A and B and radius 2 units touch each other externally at ‘C’. A third circle with centre ‘C’ and radius ‘2’ units meets other two at D and E. Then the area of the quadrilateral ABDE is
-
View Hint View Answer Discuss in Forum
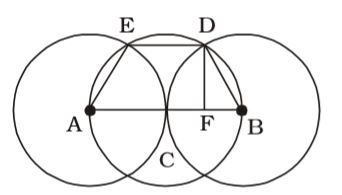
ABDE will be a trapezium
AB = 4 unitsDE = 1 AB = 2 units 2
FB = 1 unit, BD = 2 units.
⇒ DF = √2² - 1² = √3units∴ Area of ABDE = 1 (AB + DE) × DF 2 = 1 (4 + 2) × √3 2
= 3√3 sq. unitsCorrect Option: B

ABDE will be a trapezium
AB = 4 unitsDE = 1 AB = 2 units 2
FB = 1 unit, BD = 2 units.
⇒ DF = √2² - 1² = √3units∴ Area of ABDE = 1 (AB + DE) × DF 2 = 1 (4 + 2) × √3 2
= 3√3 sq. units

