166. The volume of air in a room is 204 m³. The height of the room is 6 m. What is the floor area of the room ?
     

1. 1. 32 m²
      

   
   
   

   2. 46 m²
      

   
   
   

   3. 44 m²
      

   
   
   

   4. 34 m²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Area of the floor =	Volume of room
   	Height of room

   
   

   =	204	= 34 sq.m.
   	6

   Correct Option: D

   Area of the floor =	Volume of room
   	Height of room

   
   

   =	204	= 34 sq.m.
   	6

---

167. The slant height of a conical mountain is 2.5 km and the area of its base is 1.54 km². (Taking π = 22/7) , the height of the mountain is :
     

1. 1. 2.2 km
      

   
   
   

   2. 2.4 km
      

   
   
   

   3. 3 km
      

   
   
   

   4. 3.11 km

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Area of the base of mountain = πr² 22 7 2r
   

   1.54 km² =	22	r²
   	7

   
   

   ⇒	1.54 × 7	= r²
   	22

   
   ⇒ 0.49 = r²
   7there4; r = 0.7 km
   Slant height = 2.5 km
   ∴ Height of the mountain = √(2.5)² - (0.7)²
   = √6.25 0.49
   = √5.76 = 2.4 km

   Correct Option: B

   Area of the base of mountain = πr² 22 7 2r
   

   1.54 km² =	22	r²
   	7

   
   

   ⇒	1.54 × 7	= r²
   	22

   
   ⇒ 0.49 = r²
   7there4; r = 0.7 km
   Slant height = 2.5 km
   ∴ Height of the mountain = √(2.5)² - (0.7)²
   = √6.25 0.49
   = √5.76 = 2.4 km

---

---

168. The base of a conical tent is 19.2 metres in diameter and the height of its vertex is 2.8 metres. The area of the canvas required to put up such a tent (in square metres) (taking π = 22/7) is nearly.
     

1. 1. 3017.1
      

   
   
   

   2. 3170
      

   
   
   

   3. 301.7
      

   
   
   

   4. 30.17

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Radius of base (r) = 19.2 ÷ 2 = 9.6 m Height (h)
   = 2.8 m Slant height
   l = √r² + h²
   = √(9.6)² + (2.8)² = √92.16 + 7.84
   = √100 = 10 m
   ∴ Required area = curved surface area = πrl
   

   =	22	× 9.6 × 10sq.m
   	7

   
   = 301.7 sq.m.

   Correct Option: C

   Radius of base (r) = 19.2 ÷ 2 = 9.6 m Height (h)
   = 2.8 m Slant height
   l = √r² + h²
   = √(9.6)² + (2.8)² = √92.16 + 7.84
   = √100 = 10 m
   ∴ Required area = curved surface area = πrl
   

   =	22	× 9.6 × 10sq.m
   	7

   
   = 301.7 sq.m.

---

169. If S denotes the area of the curved surface of a right circular cone of height h and semivertical angle a then S equals
     

1. 1. πh² tan²α
      

   
   
   

   2. 	1	πh² tanα
      	3

      
      

   
   
   

   3. πh² secα tanα
      

   
   
   

   4. 	1	πh² secα tanα
      	3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
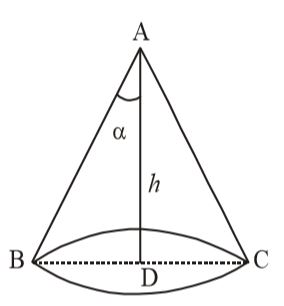
   AD = h
   

   tan α =	BD
   	AD

   
   ⇒ BD = h tanα
   ∴ Radius (r) = h tanα
   ∴ l = √h² + r²
   = √h² + h² tan²α
   = √h² (1 + tan²α)
   = √h² sec²α = h secα
   ∴ Curved Surface area of the circular cone = πrl
   = π × h tanα . h secα
   = πh² secα. tanα

   Correct Option: C

   
   AD = h
   

   tan α =	BD
   	AD

   
   ⇒ BD = h tanα
   ∴ Radius (r) = h tanα
   ∴ l = √h² + r²
   = √h² + h² tan²α
   = √h² (1 + tan²α)
   = √h² sec²α = h secα
   ∴ Curved Surface area of the circular cone = πrl
   = π × h tanα . h secα
   = πh² secα. tanα

---

---

170. The height and the radius of the base of a right circular cone are 12 cm and 6cm respectively. The radius of the circular cross-section of the cone cut by a plane parallel to its base at a distance of 3 cm from the base is
     

1. 1. 4 cm
      

   
   
   

   2. 5.5 cm
      

   
   
   

   3. 4.5 cm
      

   
   
   

   4. 3.5 cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
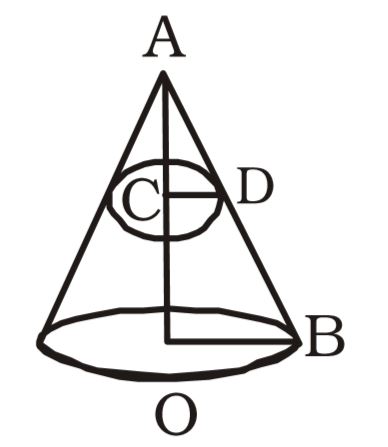
   AC = 12 – 3 = 9 cm
   OB = 6cm
   ∆ACD ~ AOB
   

   ⇒	AC	=	CD
   	OA		OB

   
   

   ⇒	9	=	CD
   	12		6

   
   

   ⇒ CD =	9	× 6 = 4.5 cm.
   	12

   Correct Option: C

   
   AC = 12 – 3 = 9 cm
   OB = 6cm
   ∆ACD ~ AOB
   

   ⇒	AC	=	CD
   	OA		OB

   
   

   ⇒	9	=	CD
   	12		6

   
   

   ⇒ CD =	9	× 6 = 4.5 cm.
   	12

---