231. If the ratio of volumes of two cones is 2 : 3 and the ratio of the radii of their bases is 1 : 2, then the ratio of their heights will be
     

1. 1. 8 : 3
      

   
   
   

   2. 3 : 8
      

   
   
   

   3. 4 : 3
      

   
   
   

   4. 3 : 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ⇒	1	πr1²h1	=					×
   	3				r1		²		h1
   	1	πr2²h2			r2				h2
   	3

   
   

   ⇒	2	=		1		²	×	h1
   	3			2				h2

   
   

   ⇒	h1	=	2	× 4 =	8	= 8 : 3
   	h2		3		3

   Correct Option: A

   ⇒	1	πr1²h1	=					×
   	3				r1		²		h1
   	1	πr2²h2			r2				h2
   	3

   
   

   ⇒	2	=		1		²	×	h1
   	3			2				h2

   
   

   ⇒	h1	=	2	× 4 =	8	= 8 : 3
   	h2		3		3

---

232. Two cubes have their volumes in the ratio 27 : 64. The ratio of their surface areas is
     

1. 1. 9 : 25
      

   
   
   

   2. 16 : 25
      

   
   
   

   3. 9 : 16
      

   
   
   

   4. 4 : 9

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Edges of cubes = x andyunits (let)
   

   ∴ Ratio of volumes =	x³
   	y³

   
   

   ∴	x³	=	27	⇒	x	=	3
   	y³		64		y		4

   
   

   ∴ Raito of surface areas =	6x³
   	6y³

   
   

   ∴	x²	=		3		²	=	9
   	y²			4				16

   Correct Option: C

   Edges of cubes = x andyunits (let)
   

   ∴ Ratio of volumes =	x³
   	y³

   
   

   ∴	x³	=	27	⇒	x	=	3
   	y³		64		y		4

   
   

   ∴ Raito of surface areas =	6x³
   	6y³

   
   

   ∴	x²	=		3		²	=	9
   	y²			4				16

---

---

233. The radius of the base and the height of a right circular cone are doubled. The volume of the cone will be
     

1. 1. 8 times of the previous volume
      

   
   
   

   2. three times of the previous volume
      

   
   
   

   3. 32 times of the previous volume
      

   
   
   

   4. 6 times of the previous volume

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Volume of a cone =	1	πr²h
   	3

   
   Again, r₁ = 2r, h₁ = 2h
   

   ∴ Volume of the second cone =	1	πr1²h1
   	3

   
   

   ∴ Volume of the second cone =	1	π(2r)² × (2h)
   	3

   
   

   ∴ Volume of the second cone =	1	πr²h × 8
   	3

   
   = Eight times of the previous volume

   Correct Option: A

   Volume of a cone =	1	πr²h
   	3

   
   Again, r₁ = 2r, h₁ = 2h
   

   ∴ Volume of the second cone =	1	πr1²h1
   	3

   
   

   ∴ Volume of the second cone =	1	π(2r)² × (2h)
   	3

   
   

   ∴ Volume of the second cone =	1	πr²h × 8
   	3

   
   = Eight times of the previous volume

---

234. A right circular cylinder is circumscribed about a hemisphere so that they share the same base. The ratio of the volumes of cylinder and hemisphere is
     

1. 1. 4 : 3
      

   
   
   

   2. 3 : 1
      

   
   
   

   3. 3 : 4
      

   
   
   

   4. 3 : 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
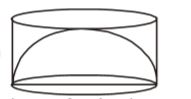
   Radius of cylinder = radius of hemisphere = r units
   

   ∴ Required ratio = πr².r :	2	πr³
   	3

   
   = 3 : 2

   Correct Option: D

   
   Radius of cylinder = radius of hemisphere = r units
   

   ∴ Required ratio = πr².r :	2	πr³
   	3

   
   = 3 : 2

---

---

235. Three cubes of sides 6 cm, 8 cm and 1 cm are melted to form a new cube. The surface area of the new cube is
     

1. 1. 486 cm²
      

   
   
   

   2. 496 cm²
      

   
   
   

   3. 586 cm²
      

   
   
   

   4. 658 cm²

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Volume of the new cube = [(6)³ + (8)³ + (1)³] cu.cm.
   = (216 + 512 + 1) cu.cm. = 729 cu.cm.
   Edge of new cube = ³√729 = 9 cm
   Its surface area = 6 × (edge)² = 6 × 9 × 9 = 486 sq. cm.

   Correct Option: A

   Volume of the new cube = [(6)³ + (8)³ + (1)³] cu.cm.
   = (216 + 512 + 1) cu.cm. = 729 cu.cm.
   Edge of new cube = ³√729 = 9 cm
   Its surface area = 6 × (edge)² = 6 × 9 × 9 = 486 sq. cm.

---