746. The edges of a rectangular box are in the ratio 1 : 2 : 3 and its surface area is 88 cm². The volume of the box is
     

1. 1. 24 cm³
      

   
   
   

   2. 48 cm³
      

   
   
   

   3. 64 cm³
      

   
   
   

   4. 120 cm³

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Sides of the box = x, 2x and 3x cm
   ∴ 2 (x × 2x + 2x × 3x + 3x × x) = 88
   ⇒ 11x² = 44
   ⇒ x² = 4
   ⇒ x = 2
   ∴ Volume of the box = x × 2x × 3x
   = 6x³ = 6 × 8 = 48 cu.cm.

   Correct Option: B

   Sides of the box = x, 2x and 3x cm
   ∴ 2 (x × 2x + 2x × 3x + 3x × x) = 88
   ⇒ 11x² = 44
   ⇒ x² = 4
   ⇒ x = 2
   ∴ Volume of the box = x × 2x × 3x
   = 6x³ = 6 × 8 = 48 cu.cm.

---

747. A right triangle with sides 3 cm, 4 cm and 5 cm is rotated about the side 3 cm to form a cone, The volume of the cone so formed is
     

1. 1. 16 π cm³
      

   
   
   

   2. 12 π cm³
      

   
   
   

   3. 15 π cm³
      

   
   
   

   4. 20 π cm³

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Clearly, r = 4 cm, h = 3cm.
   

   ∴ Volume of cone =	1	πr²h
   	3

   
   

   =	1	π × 16 × 3 = 16π cm³
   	3

   Correct Option: A

   Clearly, r = 4 cm, h = 3cm.
   

   ∴ Volume of cone =	1	πr²h
   	3

   
   

   =	1	π × 16 × 3 = 16π cm³
   	3

---

---

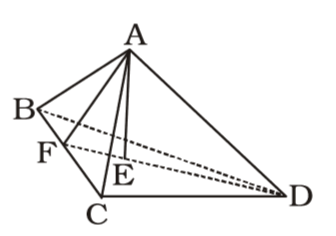
748. If the length of each side of a regular tetrahedron is 12 cm, then the volume of the tetrahedron is
     

1. 1. 144√2 cu. cm.
      

   
   
   

   2. 72√2 cu. cm.
      

   
   
   

   3. 8√2 cu. cm.
      

   
   
   

   4. 12√2 cu. cm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Volume of the tetrahedron =	1	Area of Base × height
   	3

   
   

   ∴ Area of the base =	√3	× 12 × 12 = 36√3 sq cm
   	4

   
   A regular tetrahedron is made up of 4 equilateral triangles.
   One is the base triangles and other are the 3 faces.
   
   In ∆DBC, draw DF ⊥ BC. ∆DBC is are equilateral triangle. DF (perpendicular) [DF 1 AF]
   = √DC² - FC² = √12² - 6²
   = √18 × 6
   = 6√3 = AF [altitude of ∆ABC]
   [∆ABC is also an equilateral ∆ with side 12cm].
   

   FE =	1	× 6√3 = 2√3 cm.
   	100

   
   [E is the centroid].
   ∴ AE = √AF² - FE²
   = √(6√3)² - (2√3)²
   = √108 - 12 = √96 = 4√6 cm
   

   ∴ Required volume =	1	× 36√3 = 4√3
   	3

   
   = 144√2 cu.cm.

   Correct Option: A

   Volume of the tetrahedron =	1	Area of Base × height
   	3

   
   

   ∴ Area of the base =	√3	× 12 × 12 = 36√3 sq cm
   	4

   
   A regular tetrahedron is made up of 4 equilateral triangles.
   One is the base triangles and other are the 3 faces.
   
   In ∆DBC, draw DF ⊥ BC. ∆DBC is are equilateral triangle. DF (perpendicular) [DF 1 AF]
   = √DC² - FC² = √12² - 6²
   = √18 × 6
   = 6√3 = AF [altitude of ∆ABC]
   [∆ABC is also an equilateral ∆ with side 12cm].
   

   FE =	1	× 6√3 = 2√3 cm.
   	100

   
   [E is the centroid].
   ∴ AE = √AF² - FE²
   = √(6√3)² - (2√3)²
   = √108 - 12 = √96 = 4√6 cm
   

   ∴ Required volume =	1	× 36√3 = 4√3
   	3

   
   = 144√2 cu.cm.

---

749. Two right circular cylinders of equal volume have their heights in the ratio 1 : 2. The ratio of their radii is :
     

1. 1. √2 : 1
      

   
   
   

   2. 2 : 1
      

   
   
   

   3. 1 : 2
      

   
   
   

   4. 1 : 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   Let radius are r₁ and r₂ respectively, then πr_{1²h1 = πr2²h2where h1 and h2 are heights
   According to question, h1 : h2 = 1 : 2
   ∴ r1 : r2 = √h2 : h1 = √2 : 1
   = √2 : 1}

   Correct Option: A

   
   Let radius are r₁ and r₂ respectively, then πr_{1²h1 = πr2²h2where h1 and h2 are heights
   According to question, h1 : h2 = 1 : 2
   ∴ r1 : r2 = √h2 : h1 = √2 : 1
   = √2 : 1}

---

---

750. The height of a triangle is increased by 10%. To retain the original area of the triangle, its corresponding base must be decreased by
     

1. 1. 10%
      

   
   
   

   2. 9	1	%
      	7

      
      

   
   
   

   3. 9	1	%
      	8

   
   
   

   4. 9	1	%
      	11

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Required per cent =	10	× 100 =	100	= 9	1	%
   	100 + 10		11		11

   Correct Option: D

   Required per cent =	10	× 100 =	100	= 9	1	%
   	100 + 10		11		11

---