-
Three equal circles of unit radius touch one another. Then the area of the circle circumscribing the three circles is
-
- 6π(2 + √3)²
-
π (2 + √3)² 6 -
π (2 + √3)² 3 - 3π(2 + √3)²
Correct Option: C
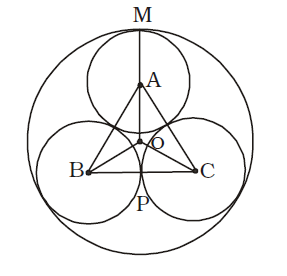
AB = BC = AC = 2 cm.
(∵ Radius of each circle = 1 cm.)
| ∴ AP = | × 2 = √3 cm. | |
| 2 |
Point O is the centroid.
| OA = | × √3 = | ||
| 3 | √3 |
| OM = | + 1 = | cm. | ||
| √3 | √3 |
OM = radius of larger circle
∴ Required area = πR²
| = |  |  | ² | |
| √3 |
| = | (2 + √3)² | |
| 3 |

