C1 and C2 are two concentric circles with centre at O. Their

Home » Aptitude » Mensuration » Question

C₁ and C₂ are two concentric circles with centre at O. Their radii are 12 cm. and 3 cm. respectively. B and C are the point of contact of two tangents drawn to C₂ from a point A lying on the circle C₁. Then, the area of the quadrilateral ABOC is

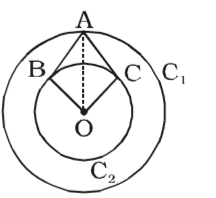
AB = AC = tangents from the same point
OB = OC = 3 cm
OA = 12 cm
∠ABO = 90°
∴ AB = √12² - 3²
= √15 × 9 = 3√15

∆ OAB =	1	OB × AB
	2

∴	1	× 3 × 3√15 =	9√15
	2		2

∴ Area of OABC =	9√15	sq.cm.
	2

9√15	sq. cm.
2