-
ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
-
- area (∆BCP) = area (∆DPQ)
- area (∆BCP) > area (∆DPQ)
- area (∆BCP) < area (∆DPQ)
- area (∆BCP) + area (∆DPQ) = area (∆BCD)
- area (∆BCP) = area (∆DPQ)
Correct Option: A
Join AC & DQ Q
∆APC and ∆BCP lie on the same base PC and between the same parallels AB and PC
∴ ar(∆APC) = ar(∆BCP)
Now, AD || CQ and AD = CQ ...(i)
∴ ADQC is a parallelogram.
Again ∆ADC and ∆DAQ are on the same base AD and between same parallels AD and CQ.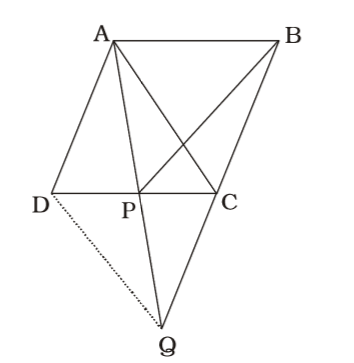
∴ ar(∆ADC) = ar(∆ADQ) Subtracting ar (DAP) from both sides, we get
ar(∆APC) = ar(∆DPQ) ...(ii)
From (i) and (ii),
we get ar(∆BPC) = ar(∆DPQ)

