Trigonometry
- From an aeroplane just over a straight road, the angles of depression of two consecutive kilometre stones situated at opposite sides of the aeroplane were found to be 60° and 30° respectively. The height (in km) of the aeroplane from the road at that instant was (Given √3 = 1.732)
-
View Hint View Answer Discuss in Forum

OC = Height of plane = h km (let)
∠DOA = ∠OAC = 60° ;
∠BOE = ∠OBC = 30°
AB = 2 km.
AC = x km (let)
∴ BC = (2 – x ) km.
From, ∆OACtan 60° = OC AC ⇒ √3
=h x ⇒ x =
=h km. ...(i) √3
From ∆OBC,tan 30° = OC CB ⇒ 1 = h √3 2 - x ⇒√3
h = 2 –h [From equation(i)] √3
[From equation(i)]⇒√3
h +h = 2 √3 ⇒ 3h + h = 2 √3
⇒ 4h = 2 √3⇒ h = 2√3 = √3 km. 4 2 = 1.732 = 0.866 km. 2 Correct Option: D

OC = Height of plane = h km (let)
∠DOA = ∠OAC = 60° ;
∠BOE = ∠OBC = 30°
AB = 2 km.
AC = x km (let)
∴ BC = (2 – x ) km.
From, ∆OACtan 60° = OC AC ⇒ √3
=h x ⇒ x =
=h km. ...(i) √3
From ∆OBC,tan 30° = OC CB ⇒ 1 = h √3 2 - x ⇒√3
h = 2 –h [From equation(i)] √3
[From equation(i)]⇒√3
h +h = 2 √3 ⇒ 3h + h = 2 √3
⇒ 4h = 2 √3⇒ h = 2√3 = √3 km. 4 2 = 1.732 = 0.866 km. 2
- From an aeroplane just over a straight road, the angles of depression of two consecutive kilometre stones situated at opposite sides of the aeroplane were found to be 60° and 30° respectively. The height (in km) of the aeroplane from the road at that instant, is
-
View Hint View Answer Discuss in Forum

A = Position of aeroplane
B and C are km stones,
∠ABD = 60°, ∠ACD = 30°
BD = x km.
∴ CD = (1 – x) km.
In ∆ABD,tan 60° = AD BD ⇒ √3
=AD x
⇒ AD = √3 x km. ...(i)
In ∆ACD,tan 30° = AD CD ⇒ 1 = AD √3 1 - x ⇒ AD = 1 - x km. ...(ii) √3
∴ From equations (i) and (ii),√3
x =1 - x √3
⇒ 3x = 1 – x&rArrr; 4x = 1 ⇒ x = 1 km. 4 ∴ AD = √3
x =√3 km. 4 Correct Option: C

A = Position of aeroplane
B and C are km stones,
∠ABD = 60°, ∠ACD = 30°
BD = x km.
∴ CD = (1 – x) km.
In ∆ABD,tan 60° = AD BD ⇒ √3
=AD x
⇒ AD = √3 x km. ...(i)
In ∆ACD,tan 30° = AD CD ⇒ 1 = AD √3 1 - x ⇒ AD = 1 - x km. ...(ii) √3
∴ From equations (i) and (ii),√3
x =1 - x √3
⇒ 3x = 1 – x&rArrr; 4x = 1 ⇒ x = 1 km. 4 ∴ AD = √3
x =√3 km. 4
- From the top of a light-house at a height 20 metres above sea-level, the angle of depression of a ship is 30°. The distance of the ship from the foot of the light house is
-
View Hint View Answer Discuss in Forum

AB = Height of light house = 20 metre
∠DAC = ∠ACB = 30°
In ∆ABC,tan 30° = AB BC ⇒ 1 = h 20 BC
⇒ BC = 20√3 metre
Correct Option: B

AB = Height of light house = 20 metre
∠DAC = ∠ACB = 30°
In ∆ABC,tan 30° = AB BC ⇒ 1 = h 20 BC
⇒ BC = 20√3 metre
- From an aeroplane just over a river, the angle of depression of two palm trees on the opposite bank of the river are found to be 60° and 30° respectively. If the breadth of the river is 400 metres, then the height of the aeroplane above the river at that instant is (Assume √3 = 1.732)
-
View Hint View Answer Discuss in Forum
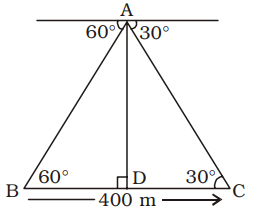
BC = River = 400 metre
AD = Height of plane = h metre
BD = x metre (let)
∴ CD = (400 – x) metre
From ∆ABDtan 60° = AD BD ⇒√ 3 = 4 x
⇒ h = √3 x metre⇒x = h metre ...(i) √3
From ∆ACD,tan 30° = AD CD ⇒ 1 = h √3 400 - x
⇒ √3h = 400 – x⇒√3h
= 400 -h √3
[From equation (i)]⇒√3h
+h = 400 √3 ⇒ 3h + h = 400 √3
⇒ 4h = 400 √3⇒ h = 400√3 4
= 100 √3 metre
= 100 × 1.732 = 173.2 metreCorrect Option: A

BC = River = 400 metre
AD = Height of plane = h metre
BD = x metre (let)
∴ CD = (400 – x) metre
From ∆ABDtan 60° = AD BD ⇒√ 3 = 4 x
⇒ h = √3 x metre⇒x = h metre ...(i) √3
From ∆ACD,tan 30° = AD CD ⇒ 1 = h √3 400 - x
⇒ √3h = 400 – x⇒√3h
= 400 -h √3
[From equation (i)]⇒√3h
+h = 400 √3 ⇒ 3h + h = 400 √3
⇒ 4h = 400 √3⇒ h = 400√3 4
= 100 √3 metre
= 100 × 1.732 = 173.2 metre
- From the peak of a hill which is 300 m high, the angle of depression of two sides of a bridge lying on a ground are 45° and 30° (both ends of the bridge are on the same side of the hill). Then the length of the bridge is
-
View Hint View Answer Discuss in Forum

AB = hill = 300 metre
CD = bridge = x metre
In ∆ABC,tan 45° = AB BC ⇒ 1 = 300 BC
⇒ BC = 300 metre
In ∆ABD,tan 30° = AB BD ⇒ 1 = 300 √3 300 + x
⇒ 300 + x = 300 √3
⇒ x = 300 √3 – 300
= 300 ( √3 – 1) metreCorrect Option: A

AB = hill = 300 metre
CD = bridge = x metre
In ∆ABC,tan 45° = AB BC ⇒ 1 = 300 BC
⇒ BC = 300 metre
In ∆ABD,tan 30° = AB BD ⇒ 1 = 300 √3 300 + x
⇒ 300 + x = 300 √3
⇒ x = 300 √3 – 300
= 300 ( √3 – 1) metre

