Trigonometry
- If 0° < θ < 90° and 2 secθ = 3 cosec²θ , then θ is
-
View Hint View Answer Discuss in Forum
2 secθ = 3cosec²θ
⇒ 2 = 3 = 3 cos θ sin² θ 1 - cos² θ
⇒ 2 – 2cos² θ = 3cos θ
⇒ 2cos² θ + 3cos θ – 2 = 0
⇒ 2cos² θ + 4cos θ – cos θ – 2 = 0
⇒ 2cosθ (cosθ + 2) –1 (cosθ + 2)
= 0
⇒ (2cosθ – 1) (cosθ + 2) = 0
∴ 2cosθ – 1 = 0 as cosθ + 2 ≠ 0⇒ cos θ - 1 = cos 60° or cos π 2 3 ⇒ θ = π 3
Correct Option: C
2 secθ = 3cosec²θ
⇒ 2 = 3 = 3 cos θ sin² θ 1 - cos² θ
⇒ 2 – 2cos² θ = 3cos θ
⇒ 2cos² θ + 3cos θ – 2 = 0
⇒ 2cos² θ + 4cos θ – cos θ – 2 = 0
⇒ 2cosθ (cosθ + 2) –1 (cosθ + 2)
= 0
⇒ (2cosθ – 1) (cosθ + 2) = 0
∴ 2cosθ – 1 = 0 as cosθ + 2 ≠ 0⇒ cos θ - 1 = cos 60° or cos π 2 3 ⇒ θ = π 3
-
View Hint View Answer Discuss in Forum
Expression
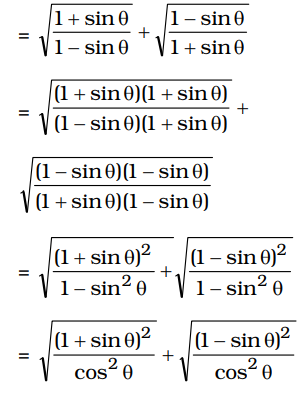
= 1 + sin θ + 1 - sin θ cos θ cos θ = 1 + sin θ + 1 - sin θ + 2 cos θ cos θ
= 2 secθCorrect Option: D
Expression
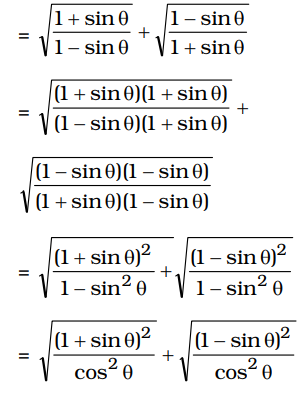
= 1 + sin θ + 1 - sin θ cos θ cos θ = 1 + sin θ + 1 - sin θ + 2 cos θ cos θ
= 2 secθ
- A person from the top of a hill observes a vehicle moving towards him at a uniform speed. It takes 10 minutes for the angle of depression to change from 45° to 60°. After this the time required by the vehicle to reach the bottom of the hill is
-
View Hint View Answer Discuss in Forum

AB = height of hill = h metre
Let speed of vehicle be v metre/minute.
Time taken to reach B from D = t minutes
CD = 10v metre
BD = vt metre
In ∆ ABC,tan 45° = AB BC ⇒ 1 = h metre BC
⇒ BC = h
= (10v + vt) metre ....(i)
In ∆ABD,tan 60° = AB BD ⇒ √3
=h vt
⇒ h = √3 vt
⇒ 10v + vt = √3 vt
⇒ 10 = √3 t – t
⇒ 10 = t (√3 - 1)⇒ t
=10 √3- 1 = 10(√3 + 1) = 10(√3 + 1) (√3 - 1)(√3 + 1) 2
= 5 (1.732 + 1) = 5 × 2.732
= 13.66 minutes
= 13 minutes 40 secondsCorrect Option: C

AB = height of hill = h metre
Let speed of vehicle be v metre/minute.
Time taken to reach B from D = t minutes
CD = 10v metre
BD = vt metre
In ∆ ABC,tan 45° = AB BC ⇒ 1 = h metre BC
⇒ BC = h
= (10v + vt) metre ....(i)
In ∆ABD,tan 60° = AB BD ⇒ √3
=h vt
⇒ h = √3 vt
⇒ 10v + vt = √3 vt
⇒ 10 = √3 t – t
⇒ 10 = t (√3 - 1)⇒ t
=10 √3- 1 = 10(√3 + 1) = 10(√3 + 1) (√3 - 1)(√3 + 1) 2
= 5 (1.732 + 1) = 5 × 2.732
= 13.66 minutes
= 13 minutes 40 seconds
- The value of

-
View Hint View Answer Discuss in Forum
(2 cos²θ – 1)

1 + tanθ + 1 - tanθ 
1 - tanθ 1 + tanθ
= (2 cos²θ – 1)
(1 + tanθ)² + (1 - tanθ)² 
1 - tan²θ
= (2 cos²θ – 1)
= 2sec² θ.cos² θ(2cos² θ - 1) 2cos² θ - 1
= 2Correct Option: D
(2 cos²θ – 1)

1 + tanθ + 1 - tanθ 
1 - tanθ 1 + tanθ
= (2 cos²θ – 1)
(1 + tanθ)² + (1 - tanθ)² 
1 - tan²θ
= (2 cos²θ – 1)
= 2sec² θ.cos² θ(2cos² θ - 1) 2cos² θ - 1
= 2
- If tan 7θ tan 2θ = 1, then the value of tan 3θ is
-
View Hint View Answer Discuss in Forum
tan 7θ . tan 2θ = 1
⇒ tan 7θ = 1 = cot 2θ tan 2θ
⇒ tan 7θ = tan (90° – 2θ)
⇒ 7θ = 90° – 2θ
⇒ 9θ = 90° ⇒ θ = 10°∴ tan 3θ = tan 30° = 1 √3
Correct Option: C
tan 7θ . tan 2θ = 1
⇒ tan 7θ = 1 = cot 2θ tan 2θ
⇒ tan 7θ = tan (90° – 2θ)
⇒ 7θ = 90° – 2θ
⇒ 9θ = 90° ⇒ θ = 10°∴ tan 3θ = tan 30° = 1 √3


