Trigonometry
- Two men standing on same side of a pillar 75 metre high, observe the angles of elevation of the top of the pillar to be 30° and 60° respectively. The distance between two men is :
-
View Hint View Answer Discuss in Forum

AB = Height of pole = 75 metre
C and D ⇒ positions of persons
Let, BC = x metre, BD = y metre
∆ACB = 60°; ∆ADB = 30°
In ∆ABC,tan60° = AB BC ⇒ √3 = 75 x ⇒ x = 75 = 25 √3 metre √3
In ∆ABDtan30° = AB BD ⇒ 1 = 75 √3 y
⇒ y = 75 √3 metre
∴ CD = y – x = (75 √3 - 25 √3) metre CD = 50√3 metreCorrect Option: C

AB = Height of pole = 75 metre
C and D ⇒ positions of persons
Let, BC = x metre, BD = y metre
∆ACB = 60°; ∆ADB = 30°
In ∆ABC,tan60° = AB BC ⇒ √3 = 75 x ⇒ x = 75 = 25 √3 metre √3
In ∆ABDtan30° = AB BD ⇒ 1 = 75 √3 y
⇒ y = 75 √3 metre
∴ CD = y – x = (75 √3 - 25 √3) metre CD = 50√3 metre
- From a point P on a level ground, the angle of elevation to the top of the tower is 30°. If the tower is 100 metre high, the distance of point P from the foot of the tower is (Take √3 = 1.73)
-
View Hint View Answer Discuss in Forum

Let, AB = Height of tower = 100 metre
∆ACB = 30°
In ∆ABC,tan30° = AB BC ⇒ 1 = 100 √3 BC
⇒ BC = 100√3 metre = (100 × 1.73) metre = 173 metre
Correct Option: C

Let, AB = Height of tower = 100 metre
∆ACB = 30°
In ∆ABC,tan30° = AB BC ⇒ 1 = 100 √3 BC
⇒ BC = 100√3 metre = (100 × 1.73) metre = 173 metre
- If the angle of elevation of the top of a pillar from the ground level is raised from 30° to 60°, the length of the shadow of a pillar of height 50 √3 will be decreased by
-
View Hint View Answer Discuss in Forum
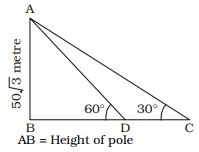
AB = Height of pole = 50 √3 metre
BC = Length of shadow = x metre
When, ∠ACB = 30°
BD = Length of shadow = y metre
when, ∠ADB = 60°
In ∆ABC,tan30° = AB BC ⇒ 1 = 50 √3 √3 x
⇒ x = 50√3 × √3 = 150 metre
In ∆ABDtan60° = AB BD ⇒ √3 = 50 √3 y ⇒ y = 50 √3 = 50 metre √3
∴ CD = x – y = 150 – 50 = 100 metreCorrect Option: C

AB = Height of pole = 50 √3 metre
BC = Length of shadow = x metre
When, ∠ACB = 30°
BD = Length of shadow = y metre
when, ∠ADB = 60°
In ∆ABC,tan30° = AB BC ⇒ 1 = 50 √3 √3 x
⇒ x = 50√3 × √3 = 150 metre
In ∆ABDtan60° = AB BD ⇒ √3 = 50 √3 y ⇒ y = 50 √3 = 50 metre √3
∴ CD = x – y = 150 – 50 = 100 metre
- Find the angular elevation of the Sun when the shadow of a 15 metre long pole is (15 / √3) metre.
-
View Hint View Answer Discuss in Forum

A' ⇒ Position of sun
AB = Height of pole = 15 metreBC = Length of shadow = 15 metre √3 ∴ tanθ = AB = 15 = √3 BC (15 / √3)
⇒ tanθ = tan60°
⇒ θ = 60°Correct Option: B

A' ⇒ Position of sun
AB = Height of pole = 15 metreBC = Length of shadow = 15 metre √3 ∴ tanθ = AB = 15 = √3 BC (15 / √3)
⇒ tanθ = tan60°
⇒ θ = 60°
- At 129 metre away from the foot of a cliff on level of ground, the angle of elevation of the top of the cliff is 30°. The height of this cliff is :
-
View Hint View Answer Discuss in Forum

AB = Height of cliff = h metre
BC = 129 metre
In ∆ABC,tan θ = AB BC ⇒ tan 30° = h 129 ⇒ 1 = h √3 129 ⇒ h = 129 = 43√3 metre √3
Correct Option: C

AB = Height of cliff = h metre
BC = 129 metre
In ∆ABC,tan θ = AB BC ⇒ tan 30° = h 129 ⇒ 1 = h √3 129 ⇒ h = 129 = 43√3 metre √3

