Trigonometry
- If A, B and C be the angles of a triangle, then put of the following, the incorrect relation is :
-
View Hint View Answer Discuss in Forum
A + B + C = π
⇒ A + B = π - C 2 2 2 ⇒ sin 
A + B 
2 = sin 
π - C 
2 2 = cos C 2
Similarly,cos 
A + B 
= sin C 2 2 cot 
A + B 
= tan C 2 2 tan 
A + B 
= cot C 2 2
Correct Option: C
A + B + C = π
⇒ A + B = π - C 2 2 2 ⇒ sin 
A + B 
2 = sin 
π - C 
2 2 = cos C 2
Similarly,cos 
A + B 
= sin C 2 2 cot 
A + B 
= tan C 2 2 tan 
A + B 
= cot C 2 2
- If 0 < x < (π / 2) and secx = cosecy, then the value of sin (x + y) is :
-
View Hint View Answer Discuss in Forum
secx = cosecy
⇒ cosx = siny⇒ sin 
π - x 
= siny 2 ⇒ y = π - x 2 ⇒ x + y = π 2 ∴ sin (x + y) = sin π = 1 2
Correct Option: B
secx = cosecy
⇒ cosx = siny⇒ sin 
π - x 
= siny 2 ⇒ y = π - x 2 ⇒ x + y = π 2 ∴ sin (x + y) = sin π = 1 2
-
If sec²θ tan²θ= 7 , then sec4θ - tan4θ = 12
-
View Hint View Answer Discuss in Forum
sec⊃ θ – tan⊃ θ = 1
sec⊃ θ + tan⊃ θ = 7 12
∴ sec4θ – tan4θ
= (sec⊃ θ – tan⊃ θ) (sec⊃ θ + tan⊃ θ)= 1 × 7 = 7 12 12
Correct Option: A
sec⊃ θ – tan⊃ θ = 1
sec⊃ θ + tan⊃ θ = 7 12
∴ sec4θ – tan4θ
= (sec⊃ θ – tan⊃ θ) (sec⊃ θ + tan⊃ θ)= 1 × 7 = 7 12 12
- If θ be acute angle and cos θ = (15 / 17) , then the value of cot
(90° – θ) is
-
View Hint View Answer Discuss in Forum
cos θ = 15 7 ⇒ sec θ = 1 = 17 cos θ 15
∴ cot (90° – θ) = tan θ
√sec⊃ θ - 1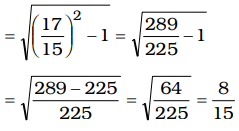
Correct Option: B
cos θ = 15 7 ⇒ sec θ = 1 = 17 cos θ 15
∴ cot (90° – θ) = tan θ
√sec⊃ θ - 1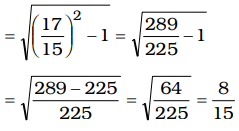
- If tan (2θ + 45°) = cot 3θ where (2θ + 45°) and 3θ are acute angles, then the value of θ is
-
View Hint View Answer Discuss in Forum
tan (2θ + 45°) = cot 3θ
= tan (90° – 3θ )
⇒ 2θ + 45° = 90° – 3θ
⇒ 5θ = 90° – 45° = 45°
∴ θ = 9°Correct Option: B
tan (2θ + 45°) = cot 3θ
= tan (90° – 3θ )
⇒ 2θ + 45° = 90° – 3θ
⇒ 5θ = 90° – 45° = 45°
∴ θ = 9°

