Trigonometry
- If a 48 m tall building has a shadow of 48 √3 m., then the angle of elevation of the sun is
-
View Hint View Answer Discuss in Forum
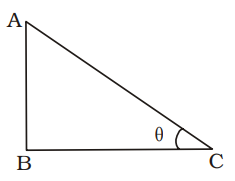
AB = Building = 48 metre
BC = Shadow = 48√3 metre
∠ACB = θ = ?
AB BC∴ tan θ = AB = 48 BC 48√3 ⇒ tanθ = 1 = tan 30° √3
θ = 30°Correct Option: D

AB = Building = 48 metre
BC = Shadow = 48√3 metre
∠ACB = θ = ?
AB BC∴ tan θ = AB = 48 BC 48√3 ⇒ tanθ = 1 = tan 30° √3
θ = 30°
- Two towers A and B have lengths 45 m and 15 m respectively. The angle of elevation from the bottom of the tower B to the top of the tower A is 60°. If the angle of elevation from the bottom of tower A to the top of the tower B is θ then value of sin θ is :
-
View Hint View Answer Discuss in Forum

PQ = Tower A = 45 metre
RS = Tower B = 15 metre,
QS = x metre (let)
∠PSQ = 60° ; ∠RQS = θ
From ∆PQS,tanθ 60° = PQ QS ⇒ √3 = 45 ⇒ √3x = 45 QS ⇒ x = 45 = 15√3 metre 5√3
From ∆RSQ,tanθ = RS = 15 QS 15√3 ⇒ tanθ = 1 √3
⇒ tanθ = tan 30°
⇒ θ = 30°
∴ sinθ = sin 30° = 1/2Correct Option: B

PQ = Tower A = 45 metre
RS = Tower B = 15 metre,
QS = x metre (let)
∠PSQ = 60° ; ∠RQS = θ
From ∆PQS,tanθ 60° = PQ QS ⇒ √3 = 45 ⇒ √3x = 45 QS ⇒ x = 45 = 15√3 metre 5√3
From ∆RSQ,tanθ = RS = 15 QS 15√3 ⇒ tanθ = 1 √3
⇒ tanθ = tan 30°
⇒ θ = 30°
∴ sinθ = sin 30° = 1/2
- A kite is flying at the height of 75 m from the ground. The string makes an angle q (where cotq = 8/15 ) with the level ground. Assuming that there is no slack in the string the length of the string is equal to :
-
View Hint View Answer Discuss in Forum

A = Position of kite
AC = length of string
AB = 75 metrecot θ = 8 15
∴ cosecθ = √1 + cot²θ= √ + 1 
8 
² = √ + 1 64 15 225 = √ 225 + 64 = √ + 1 289 225 225 = 17 15 ∴ sinθ = 17 15
From ∆ABCsinθ = AB AC ⇒ 15 = 75 17 AC
⇒ AC × 15 = 17 × 15⇒ AC = 17 × 75 = 85 metre 15 Correct Option: A

A = Position of kite
AC = length of string
AB = 75 metrecot θ = 8 15
∴ cosecθ = √1 + cot²θ= √ + 1 
8 
² = √ + 1 64 15 225 = √ 225 + 64 = √ + 1 289 225 225 = 17 15 ∴ sinθ = 17 15
From ∆ABCsinθ = AB AC ⇒ 15 = 75 17 AC
⇒ AC × 15 = 17 × 15⇒ AC = 17 × 75 = 85 metre 15
- The angle of elevation of a tower from a distance of 100 metre from its foot is 30°. Then the height of the tower is
-
View Hint View Answer Discuss in Forum

AB = Tower = h metre
From ∆ABC,tan 30° = AB BC ⇒ 1 = h √3 100 >⇒ h = 100 metre √3 Correct Option: D

AB = Tower = h metre
From ∆ABC,tan 30° = AB BC ⇒ 1 = h √3 100 >⇒ h = 100 metre √3
- A 10 metre long ladder is placed against a wall. It is inclined at an angle of 30° to the ground. The distance (in m) of the foot of the ladder from the wall is (Given √3 = 1.732)
-
View Hint View Answer Discuss in Forum

AC = ladder = 10 metre
BC = ?
∠ABC = θ = 30°
From ∆ABC,cos θ = BC AC ⇒ cos 30° = BC 10 ⇒ √3 = BC 2 10 ⇒ BC = 10√3 = 5√3 2
= 5 × 1.732 = 8.660 metreCorrect Option: D

AC = ladder = 10 metre
BC = ?
∠ABC = θ = 30°
From ∆ABC,cos θ = BC AC ⇒ cos 30° = BC 10 ⇒ √3 = BC 2 10 ⇒ BC = 10√3 = 5√3 2
= 5 × 1.732 = 8.660 metre

