96. If sin θ – cos θ = (7 / 13) and 0 < θ < 90°, then the value of sin θ + cos θ is

1. 1. 	17
      	13

   
   
   

   2. 	13
      	17

   
   
   

   3. 	1
      	13

   
   
   

   4. 	1
      	17

   
   
   

---

1. View Hint View Answer Discuss in Forum

   sin θ – cos θ =	7	......(i)
   	13

   
   sin θ + cos θ = x .....(ii)
   On squaring both equations and adding,
   

   2(sin²θ + cos²θ) =	49	+ x²
   	169

   
   

   ⇒ x² = 2 -		49	=	338 - 49
   		169		169

   
   

   =		289	⇒ x =	17
   		169		13

   
   

   Correct Option: A

   sin θ – cos θ =	7	......(i)
   	13

   
   sin θ + cos θ = x .....(ii)
   On squaring both equations and adding,
   

   2(sin²θ + cos²θ) =	49	+ x²
   	169

   
   

   ⇒ x² = 2 -		49	=	338 - 49
   		169		169

   
   

   =		289	⇒ x =	17
   		169		13

   
   

---

97. If θ be acute and tan θ + cot θ = 2, then the value of tan⁵ θ + cot¹⁰ θ is

1. 1. 1

   
   
   

   2. 2

   
   
   

   3. 3

   
   
   

   4. 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   tan θ + cot θ = 2
   

   ⇒tan θ +	1	= 2
   	tan θ

   
   ⇒ tan² θ + 1 = 2tan θ
   ⇒ tan² θ – 2tan θ + 1 = 0
   ⇒ (tan θ – 1)² = 0
   ⇒ tan θ = 1 ⇒ cot θ = 1
   ∴ tan⁵ θ + cot¹⁰ θ = 1 + 1 = 2

   Correct Option: B

   tan θ + cot θ = 2
   

   ⇒tan θ +	1	= 2
   	tan θ

   
   ⇒ tan² θ + 1 = 2tan θ
   ⇒ tan² θ – 2tan θ + 1 = 0
   ⇒ (tan θ – 1)² = 0
   ⇒ tan θ = 1 ⇒ cot θ = 1
   ∴ tan⁵ θ + cot¹⁰ θ = 1 + 1 = 2

---

---

98. The simplified value of (sec A – cos A)² + (cosec A – sin A)² – (cot A – tan A)² is

1. 1. 0

   
   
   

   2. 	1
      	2

   
   
   

   3. 1

   
   
   

   4. 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   (sec A – cosA)² + (cosec A – sinA)² – (cot A – tan A)²
   = sec²A + cos²A – 2secA cosA + cosec²A + sin²A– 2cosec A. sinA – cot²A – tan²A + 2 cotA. tanA
   = sec²A – tan²A + cos²A+ sin²A + cosec²A – cot²A – 2
   = 3 – 2 = 1
   

   Correct Option: C

   (sec A – cosA)² + (cosec A – sinA)² – (cot A – tan A)²
   = sec²A + cos²A – 2secA cosA + cosec²A + sin²A– 2cosec A. sinA – cot²A – tan²A + 2 cotA. tanA
   = sec²A – tan²A + cos²A+ sin²A + cosec²A – cot²A – 2
   = 3 – 2 = 1
   

---

99. If tan θ =		4	, then the value of	3sin θ + 2cos θ	is
    		3		3sin θ - 2cos θ

1. 1. 0.5

   
   
   

   2. –0.5

   
   
   

   3. 3.0

   
   
   

   4. –3.0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   tan θ =	4	(Given)
   	3

   
   

   ∴		3 sin θ + 2 cos θ	=	3 tan θ + 2
   		3sin θ - 2 cos θ		3 tan θ - 2

   
   [Dividing N^r & D^r by cos θ]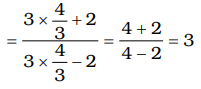
   

   Correct Option: C

   tan θ =	4	(Given)
   	3

   
   

   ∴		3 sin θ + 2 cos θ	=	3 tan θ + 2
   		3sin θ - 2 cos θ		3 tan θ - 2

   
   [Dividing N^r & D^r by cos θ]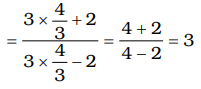
   

---

---

100. If θ be a positive acute angle satisfying cos²θ+ cos⁴ θ = 1, then the value of tan²θ+ tan⁴ θ is

1. 1. 	3
      	2

   
   
   

   2. 1

   
   
   

   3. 	1
      	2

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   cos²θ + cos⁴θ = 1
   ⇒ cos³θ = 1 – cos²θ = sin²θ
   ⇒ tan²θ = cos²θ
   ∴ tan²θ + tan³θ = cos²θ + cos³θ
   = 1

   Correct Option: B

   cos²θ + cos⁴θ = 1
   ⇒ cos³θ = 1 – cos²θ = sin²θ
   ⇒ tan²θ = cos²θ
   ∴ tan²θ + tan³θ = cos²θ + cos³θ
   = 1

---