486. The value of		sinθ + sinφ	+	cosθ − cosφ		is :
     		cosθ + cosφ		sinθ − sinφ

1. 1. 1

   
   
   

   2. 2

   
   
   

   3. 1/2

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Expression =	sinθ + sinφ	+	cosθ - cosφ
   	cosθ + cosφ		sinθ - sinφ

   
   

   =	(sinθ + sinφ)(sinθ - sinφ) + (cosθ - cosφ)(cosθ + cosφ)
   	(cosθ + cosφ)(sinθ - sinφ)

   
   

   =	sin²θ + sin²φ + cos²θ - cos²φ
   	(cosθ + cosφ)(sinθ - sinφ)

   
   

   =	(sin²θ + cos²θ) - (sinφθ + cos²φ)
   	(cosθ + cosφ)(sinθ - sinφ)

   
   

   =	1 - 1	= 0
   	(cosθ + cosφ)(sinθ - sinφ)

   Correct Option: D

   Expression =	sinθ + sinφ	+	cosθ - cosφ
   	cosθ + cosφ		sinθ - sinφ

   
   

   =	(sinθ + sinφ)(sinθ - sinφ) + (cosθ - cosφ)(cosθ + cosφ)
   	(cosθ + cosφ)(sinθ - sinφ)

   
   

   =	sin²θ + sin²φ + cos²θ - cos²φ
   	(cosθ + cosφ)(sinθ - sinφ)

   
   

   =	(sin²θ + cos²θ) - (sinφθ + cos²φ)
   	(cosθ + cosφ)(sinθ - sinφ)

   
   

   =	1 - 1	= 0
   	(cosθ + cosφ)(sinθ - sinφ)

---

487. If   tanθ =	8	, the value of	√1 − sinθ	is :
     	15		√1 + sinθ

1. 1. 1

      5

   
   
   

   2. 2

      5

   
   
   

   3. 3

      5

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   tanθ =	8
   	15

   
   ∴  sec²θ – tan²θ = 1
   ⇒  sec²θ = 1 + tan²θ
   

   = 1 +		8		2
   		15

   
   

   = 1 +	64	=	225 + 64	=	289
   	225		225		225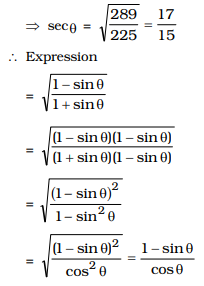

   
   
   

   =	1	−	sinθ	= secθ − tanθ
   	cosθ		cosθ

   
   

   =	17	−	8
   	15		15

   
   

   =	17 − 8	=	9	=	3
   	15		15		5

   Correct Option: C

   tanθ =	8
   	15

   
   ∴  sec²θ – tan²θ = 1
   ⇒  sec²θ = 1 + tan²θ
   

   = 1 +		8		2
   		15

   
   

   = 1 +	64	=	225 + 64	=	289
   	225		225		225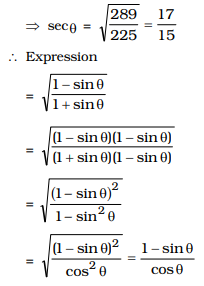

   
   
   

   =	1	−	sinθ	= secθ − tanθ
   	cosθ		cosθ

   
   

   =	17	−	8
   	15		15

   
   

   =	17 − 8	=	9	=	3
   	15		15		5

---

---

488. The value of	sinθ	+	sinθ	is :
     	1 + cosθ		1 − cosθ

1. 1. 2sinθ

   
   
   

   2. 2cosθ

   
   
   

   3. 2secθ

   
   
   

   4. 2cosecθ

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Expression =	sinθ	+	sinθ
   	1 + cosθ		1 − cosθ

   
   

   =	sinθ(1 − cosθ) + sinθ(1 + cosθ)
   	(1 + cosθ)(1 − cosθ)

   
   

   =	2sinθ	=	2	= 2cosecθ
   	sin2θ		sinθ

   Correct Option: D

   Expression =	sinθ	+	sinθ
   	1 + cosθ		1 − cosθ

   
   

   =	sinθ(1 − cosθ) + sinθ(1 + cosθ)
   	(1 + cosθ)(1 − cosθ)

   
   

   =	2sinθ	=	2	= 2cosecθ
   	sin2θ		sinθ

---

489. If tan 3θ. tan 7θ = 1, then the value of tan (θ + 36°) is :

1. 1. 1

      √3

   
   
   

   2. 0

   
   
   

   3. 1

   
   
   

   4. √3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   tan 3θ. tan 7θ = 1
   

   ⇒  tan 3θ =	1	= cot7θ
   	tan 7θ

   
   ⇒  tan3θ = tan (90° – 7θ)
   ⇒  3θ = 90° – 7θ
   ⇒  3θ + 7θ = 90°
   ⇒  10θ = 90° ⇒ θ = 9°
   ∴  tan (θ + 36°) = tan (9° + 36°)
   = tan 45° = 1

   Correct Option: C

   tan 3θ. tan 7θ = 1
   

   ⇒  tan 3θ =	1	= cot7θ
   	tan 7θ

   
   ⇒  tan3θ = tan (90° – 7θ)
   ⇒  3θ = 90° – 7θ
   ⇒  3θ + 7θ = 90°
   ⇒  10θ = 90° ⇒ θ = 9°
   ∴  tan (θ + 36°) = tan (9° + 36°)
   = tan 45° = 1

---

---

490. The value of 8 (sin⁶θ + cos⁶θ) – 12 (sin⁴θ + cos⁴θ) is equal to

1. 1. 20

   
   
   

   2. – 20

   
   
   

   3. – 4

   
   
   

   4. 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   8 (sin⁶θ + cos⁶θ) – 12 (sin⁴θ + cos⁴θ)
   = 8 {(sin²θ + cos²θ)³ – 3 sin²θ.cos²θ (sin²θ + cos²θ)} – 12 {(sin²θ + cos²θ)² – 2 sin²θcos²θ)}
   = 8 (1 – 3 sin²θ . cos²θ) – 12 (1 – 2 sin²θ.cos²θ)
   = 8 – 24 sin²θ.cos²θ – 12 + 24sin²θ.cos²θ = –4

   Correct Option: C

   8 (sin⁶θ + cos⁶θ) – 12 (sin⁴θ + cos⁴θ)
   = 8 {(sin²θ + cos²θ)³ – 3 sin²θ.cos²θ (sin²θ + cos²θ)} – 12 {(sin²θ + cos²θ)² – 2 sin²θcos²θ)}
   = 8 (1 – 3 sin²θ . cos²θ) – 12 (1 – 2 sin²θ.cos²θ)
   = 8 – 24 sin²θ.cos²θ – 12 + 24sin²θ.cos²θ = –4

---