411. Two posts are x metres apart and the height of one is double that of the other. If from the mid-point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary, then the height (in metres) of the shorter post is

1. 1. x

      2 √2

   
   
   

   2. x

      4

   
   
   

   3. x √2

   
   
   

   4. x

      √2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   CD = h metre, AB = 2h metre
   
   

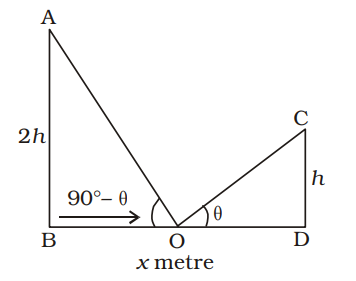
   OB = OD =	x	metre
   	2

   
   From ∆OCD,
   

   tan θ =	h	=	2h	..........(i)
   	x		x
   	2

   
   From ∆OAB,
   

   tan (90° – θ) =	AB
   	BO

   
   

   ⇒ cotθ =	2h	=	4h	..........(ii)
   	x		x
   	2

   
   Multiplying both equations,
   

   tanθ .cotθ =	2h	×	4h
   	x		x

   
   ⇒ x² = 8h²
   [∵ tanθcotθ = 1]
   

   ⇒ h2 =	x2
   	8

   
   

   ⇒ h =	x	metre
   	2√2

   Correct Option: A

   CD = h metre, AB = 2h metre
   
   

   OB = OD =	x	metre
   	2

   
   From ∆OCD,
   

   tan θ =	h	=	2h	..........(i)
   	x		x
   	2

   
   From ∆OAB,
   

   tan (90° – θ) =	AB
   	BO

   
   

   ⇒ cotθ =	2h	=	4h	..........(ii)
   	x		x
   	2

   
   Multiplying both equations,
   

   tanθ .cotθ =	2h	×	4h
   	x		x

   
   ⇒ x² = 8h²
   [∵ tanθcotθ = 1]
   

   ⇒ h2 =	x2
   	8

   
   

   ⇒ h =	x	metre
   	2√2

---

412. The angle of elevation of the top of a building and the top of the chimney on the roof of the building from a point on the ground are x and 45° respectively. The height of building is h metre. Then the height of the chimney, (in metre) is :

1. 1. h cot x + h

   
   
   

   2. h cot x – h

   
   
   

   3. h tan x – h

   
   
   

   4. h tan x + h

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   AB = Buidling = h metre
   AD = Chimney = y metre
   From ∆BCD,
   

   tan45° =	BD
   	BC

   
   

   ⇒ 1 =	h + y
   	BC

   
   ⇒ BC = h + y ..... ... (i)
   From ∆ABC,
   

   tan x =	AB
   	BC

   
   

   ⇒ tan x =	h
   	BC

   
   ⇒ BC = h cot x ...........(ii)
   From equations (i) and (ii),
   h + y = h cot x
   ⇒ y = (h cot x – h) metre

   Correct Option: B

   
   AB = Buidling = h metre
   AD = Chimney = y metre
   From ∆BCD,
   

   tan45° =	BD
   	BC

   
   

   ⇒ 1 =	h + y
   	BC

   
   ⇒ BC = h + y ..... ... (i)
   From ∆ABC,
   

   tan x =	AB
   	BC

   
   

   ⇒ tan x =	h
   	BC

   
   ⇒ BC = h cot x ...........(ii)
   From equations (i) and (ii),
   h + y = h cot x
   ⇒ y = (h cot x – h) metre

---

---

413. A telegraph post is bent at a point above the ground due to storm. Its top just meets the ground at a distance of 8 √3 metres from its foot and makes an angle of 30°, then the height of the post is :

1. 1. 16 metres

   
   
   

   2. 23 metres

   
   
   

   3. 24 metres

   
   
   

   4. 10 metres

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
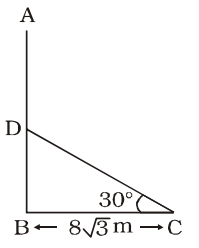
   AB = Telegraph post = h metre
   Telegraph post bends at point D.
   DB = x metre
   ∴ AD = CD = (h – x) metre
   BC = 8 √3 metre
   From, ∆ DBC,
   

   sin 30° =	DB
   	DC

   
   

   ⇒	1	=	x	⇒ 2x = h - x
   	2		h - x

   
   ⇒ 3x = h ......... (i)
   Again,
   

   tan 30° =	DB
   	BC

   
   

   ⇒	1	=	x
   	√3		8√3

   
   ⇒ x = 8 metre
   ∴ h = 3 × 8 = 24 metre

   Correct Option: C

   
   AB = Telegraph post = h metre
   Telegraph post bends at point D.
   DB = x metre
   ∴ AD = CD = (h – x) metre
   BC = 8 √3 metre
   From, ∆ DBC,
   

   sin 30° =	DB
   	DC

   
   

   ⇒	1	=	x	⇒ 2x = h - x
   	2		h - x

   
   ⇒ 3x = h ......... (i)
   Again,
   

   tan 30° =	DB
   	BC

   
   

   ⇒	1	=	x
   	√3		8√3

   
   ⇒ x = 8 metre
   ∴ h = 3 × 8 = 24 metre

---

414. Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. From a point between them on road, angle of elevation of their tops are 30° and 60°. The height of each pole (in metre) is

1. 1. 25 √3

   
   
   

   2. 20 √3

   
   
   

   3. 28 √3

   
   
   

   4. 30 √3

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   AB = CD = h metre (Height of pole)
   From ∆ABE,
   

   tan 30° =	h
   	x

   
   

   ⇒	1	=	h	⇒ √3h = x .........(i)
   	√3		x

   
   From ∆DEC,
   

   tan 60° =	h
   	100 - x

   
   

   ⇒ √3 =	h
   	100 - x

   
   ⇒ √3 ( 100 - x) = h
   ⇒ √3 (100 - √3h) = h
   [From equation (i)]
   ⇒ 100 √3 - 3h ⇒ 4h = 100√3
   ⇒ h = 25 √3 metre

   Correct Option: A

   
   AB = CD = h metre (Height of pole)
   From ∆ABE,
   

   tan 30° =	h
   	x

   
   

   ⇒	1	=	h	⇒ √3h = x .........(i)
   	√3		x

   
   From ∆DEC,
   

   tan 60° =	h
   	100 - x

   
   

   ⇒ √3 =	h
   	100 - x

   
   ⇒ √3 ( 100 - x) = h
   ⇒ √3 (100 - √3h) = h
   [From equation (i)]
   ⇒ 100 √3 - 3h ⇒ 4h = 100√3
   ⇒ h = 25 √3 metre

---

---

415. The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60°. The height of the tower is

1. 1. √3 m

   
   
   

   2. 5 √3 m

   
   
   

   3. 10 √3 m

   
   
   

   4. 20 √3 m

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
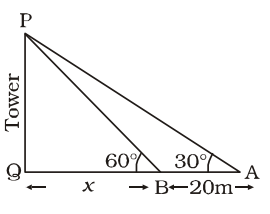
   Let PQ = h metre and BQ = x metre.
   From ∆ APQ,
   

   tan30° =	h
   	x + 20

   
   

   ⇒	1	=	h
   	√3		x + 20

   
   ⇒ √3h = x + 20 ...........(i)
   From ∆ PQB,
   

   tan 60° =	PQ	=	h
   	BQ		x

   
   

   ⇒ √3 =	h	⇒ h = √3x
   	x

   
   

   ⇒ x =	1	h .......(ii)
   	√3

   
   

   ∴ √3h =	1	h + 20
   	√3

   
   [From equation (i) and (ii)]
   ⇒ 3h – h = 20 √3
   ⇒ 2h = 20 √3
   ∴ h = 10 √3 metre

   Correct Option: C

   
   Let PQ = h metre and BQ = x metre.
   From ∆ APQ,
   

   tan30° =	h
   	x + 20

   
   

   ⇒	1	=	h
   	√3		x + 20

   
   ⇒ √3h = x + 20 ...........(i)
   From ∆ PQB,
   

   tan 60° =	PQ	=	h
   	BQ		x

   
   

   ⇒ √3 =	h	⇒ h = √3x
   	x

   
   

   ⇒ x =	1	h .......(ii)
   	√3

   
   

   ∴ √3h =	1	h + 20
   	√3

   
   [From equation (i) and (ii)]
   ⇒ 3h – h = 20 √3
   ⇒ 2h = 20 √3
   ∴ h = 10 √3 metre

---