Trigonometry
-
If tan θ = 3 , then the value of 4sin²θ - 2cos²θ is equal to 4 4sin²θ + 3cos²θ
-
View Hint View Answer Discuss in Forum
tan θ = 3 ⇒ tan² θ = 9 4 16
Expression= 4sin² θ - 2 cos² θ 4sin² θ - 3 cos² θ 
= 4tan² θ - 2 4tan² θ + 3 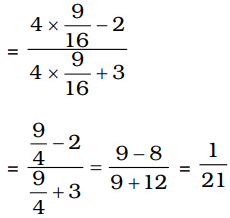
Correct Option: A
tan θ = 3 ⇒ tan² θ = 9 4 16
Expression= 4sin² θ - 2 cos² θ 4sin² θ - 3 cos² θ 
= 4tan² θ - 2 4tan² θ + 3 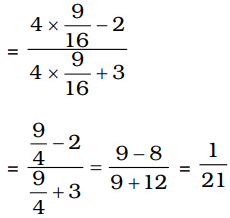
-
If cos α = a, sin α = b, then sin²β is equal to cosβ sinβ
-
View Hint View Answer Discuss in Forum
cosα = a cosβ ⇒ cos²α = a² cos²β ⇒ 1 - sin²α = a² 1 - sin²β
⇒ 1 – sin²α = α² (1 – sin²β)
⇒1 – b² sin²β = a² – a² sin²β
⇒ 1 – a² = b ²sin²β – a² sin²β
⇒ 1 – a² = (b² – a² ) sin²β⇒ sin²β = 1 - a² = a² - 1 b² - a² a² - b²
Correct Option: C
cosα = a cosβ ⇒ cos²α = a² cos²β ⇒ 1 - sin²α = a² 1 - sin²β
⇒ 1 – sin²α = α² (1 – sin²β)
⇒1 – b² sin²β = a² – a² sin²β
⇒ 1 – a² = b ²sin²β – a² sin²β
⇒ 1 – a² = (b² – a² ) sin²β⇒ sin²β = 1 - a² = a² - 1 b² - a² a² - b²
-
If cos θ = 3 then the value of sinθ . secθ . tanθ is 5
-
View Hint View Answer Discuss in Forum
cos θ = 3 5 ∴ sec θ = 5 3
∴ tan θ = √sec² θ - 1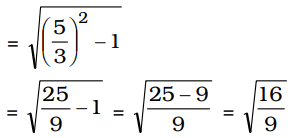
= 4 3 ∴ sinθ . secθ . tanθ = sin θ . tan θ cos θ = tan²θ = 
4 
² = 16 3 9
Correct Option: B
cos θ = 3 5 ∴ sec θ = 5 3
∴ tan θ = √sec² θ - 1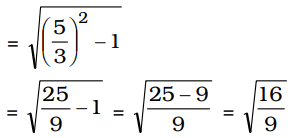
= 4 3 ∴ sinθ . secθ . tanθ = sin θ . tan θ cos θ = tan²θ = 
4 
² = 16 3 9
- If √3 tan θ = 3 sin θ, then the value of (sin²θ – cos²θ) is
-
View Hint View Answer Discuss in Forum
√3 tanθ = 3 sinθ
⇒√3 sinθ = 3 sinθ cosθ
⇒ √3 = 3 cosθ⇒ cosθ = √3 = 1 3 √3
∴ sinθ = √1 - cos²θ
= 2 - 1 = 1 3 3 3 Correct Option: C
√3 tanθ = 3 sinθ
⇒√3 sinθ = 3 sinθ cosθ
⇒ √3 = 3 cosθ⇒ cosθ = √3 = 1 3 √3
∴ sinθ = √1 - cos²θ
= 2 - 1 = 1 3 3 3
- If sin(A + B) = sin A cos B + cos A sin B, then the value of sin75° is
-
View Hint View Answer Discuss in Forum
A = 45°, B = 30° (let)
∴ sin (A + B) = sinA . cosB + cosA . sinB
⇒ sin(45° + 30°)
= sin45°. cos30° + cos45° . sin30°= 1 × √3 + 1 × 1 √2 2 √2 2 = √3 + 1 = √3 + 1 2√2 2√2 2√2
Correct Option: C
A = 45°, B = 30° (let)
∴ sin (A + B) = sinA . cosB + cosA . sinB
⇒ sin(45° + 30°)
= sin45°. cos30° + cos45° . sin30°= 1 × √3 + 1 × 1 √2 2 √2 2 = √3 + 1 = √3 + 1 2√2 2√2 2√2

