Trigonometry
- On a ground, there is a vertical tower with a flagpole on its top. At a point 9 metre away from the foot of the tower, the angles of elevation of the top and bottom of the flagpole are 60° and 30° respectively. The height of the flagpole is :
-
View Hint View Answer Discuss in Forum
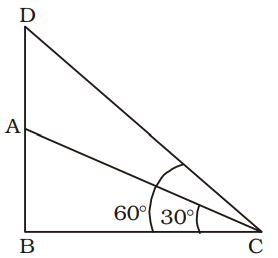
AB = Height of tower = h metre
AD = Height of flagstaff = x metre
∠BCD = 60°; ∠BCA = 30°
BC = 9 metre
In ∆ABC,tan 30° = AB BC ⇒ 1 = h √3 9 ⇒ h = 9 = 3√3 metre √3
In ∆BCD,tan 60° = BD BC ⇒ √3 = h + x 9
⇒ h + x = 9 √3
⇒ 3 √3 + x = 9 √3
⇒ x = 9 √3 – 3 √3
= 6 √3 metreCorrect Option: B

AB = Height of tower = h metre
AD = Height of flagstaff = x metre
∠BCD = 60°; ∠BCA = 30°
BC = 9 metre
In ∆ABC,tan 30° = AB BC ⇒ 1 = h √3 9 ⇒ h = 9 = 3√3 metre √3
In ∆BCD,tan 60° = BD BC ⇒ √3 = h + x 9
⇒ h + x = 9 √3
⇒ 3 √3 + x = 9 √3
⇒ x = 9 √3 – 3 √3
= 6 √3 metre
- A telegraph post is bent at a point above the ground. Its top just touches the ground at a distance of 8 √3 metre from its foot and makes an angle of 30° with the horizontal. The height (in metre) of the post is :
-
View Hint View Answer Discuss in Forum
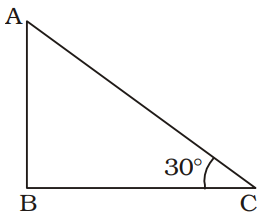
Let telegraph pole bend at point A.
BC = 8 √3 metre
In ∆ABC,tan 30° = AB BC ⇒ 1 = AB √3 8√3 ⇒ AB = 8√3 = 8 metre √3 Again, sin 30° = AB AC ⇒ 1 = 8 AC 2
⇒ AC = 2 × 8 = 16 metre
∴ Height of telegraph–pole
= AB + AC
= 8 + 16 = 24 metreCorrect Option: D

Let telegraph pole bend at point A.
BC = 8 √3 metre
In ∆ABC,tan 30° = AB BC ⇒ 1 = AB √3 8√3 ⇒ AB = 8√3 = 8 metre √3 Again, sin 30° = AB AC ⇒ 1 = 8 AC 2
⇒ AC = 2 × 8 = 16 metre
∴ Height of telegraph–pole
= AB + AC
= 8 + 16 = 24 metre
- The upper part of a tree broken at a certain height makes an angle of 60° with the ground at a distance of 10 metre from its foot. The original height of the tree was
-
View Hint View Answer Discuss in Forum
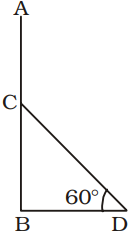
AB = Height of tree
Let the tree break at point C.
BC = x metre
∴ AC = CD
∠CDB = 60°; BD = 10 metre
In ∆BCD,tan 60° = BC ⇒ √3 = x BD 10
⇒ x = 10 √3 metreAgain, sin 60° = BC CD ⇒ √3 = 10√3 2 CD ⇒ CD = 2 × 10√3 = 20 metre √3
∴ Height of tree = AB
= (20 + 10√3) metre
= 10 (2 + √3) metreCorrect Option: C

AB = Height of tree
Let the tree break at point C.
BC = x metre
∴ AC = CD
∠CDB = 60°; BD = 10 metre
In ∆BCD,tan 60° = BC ⇒ √3 = x BD 10
⇒ x = 10 √3 metreAgain, sin 60° = BC CD ⇒ √3 = 10√3 2 CD ⇒ CD = 2 × 10√3 = 20 metre √3
∴ Height of tree = AB
= (20 + 10√3) metre
= 10 (2 + √3) metre
- The angle of elevation of the top of an unfinished pillar at a point 150 metres from its base is 30°. The height (in metres) that the pillar must be raised so that its angle of elevation at the same point may be 45°, is (Take, √3 = 1.732)
-
View Hint View Answer Discuss in Forum
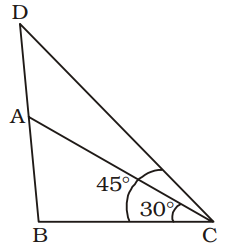
AB = incomplete pole
BC = 150 metre
∠ACB = 30°
In ∆ABC,tan30° AB BC ⇒ 1 = AB √3 150 ⇒ AB = 150 = 50√3 metre √3
In ∆BCD,tan45° = BD BC ⇒ 1 = BD 150
⇒ BD = 150 metre
∴ AD = BD – AB
= (150 – 50 √3 ) metre
= 50 (3 - √3) metre
= 50 (3 – 1.732) metre
= (50 × 1.268) metre
= 63.4 metre
Correct Option: A

AB = incomplete pole
BC = 150 metre
∠ACB = 30°
In ∆ABC,tan30° AB BC ⇒ 1 = AB √3 150 ⇒ AB = 150 = 50√3 metre √3
In ∆BCD,tan45° = BD BC ⇒ 1 = BD 150
⇒ BD = 150 metre
∴ AD = BD – AB
= (150 – 50 √3 ) metre
= 50 (3 - √3) metre
= 50 (3 – 1.732) metre
= (50 × 1.268) metre
= 63.4 metre
- The angle of elevation of the top of a tower, vertically erected in the middle of a paddy field, from two points on a horizontal line through the foot of the tower are given to be α and β (α > β). The height of the tower is h unit. A possible distance (in the same unit) between the points is
-
View Hint View Answer Discuss in Forum

Let AB = height of tower = h metre
∠ACB = α ; ∠ADB = β
In ∆ABC,tan α = AB BC ⇒ tan α = h ⇒ BC = h BC tan α
= h cotα
In ∆ABD,⇒ tan β = AB ⇒ tan β = h BD BD ⇒ BD = h = h cot β tan β
∴ BC = BC + BD
= h cotα + h cotβ
= h (cotα + cotβ)Correct Option: D

Let AB = height of tower = h metre
∠ACB = α ; ∠ADB = β
In ∆ABC,tan α = AB BC ⇒ tan α = h ⇒ BC = h BC tan α
= h cotα
In ∆ABD,⇒ tan β = AB ⇒ tan β = h BD BD ⇒ BD = h = h cot β tan β
∴ BC = BC + BD
= h cotα + h cotβ
= h (cotα + cotβ)

