Trigonometry
-
If x - tan²30° = sin²30° + 4 cot² 45° – sec² 60°, then the value of x is : 1 + tan²30°
-
View Hint View Answer Discuss in Forum
x - x tan² 30° 1 + tan² 30°
= sin²30° + 4 cot²45° – sec²60°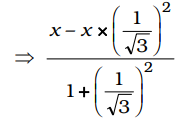
= 
1 
² + 4 × (1)² - (2)² 2 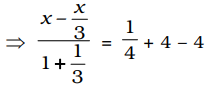
⇒ 3x - x = 1 3 + 1 4 ⇒ 2x = 1 × 4 = 1 4 ⇒ x = 1 2
Correct Option: C
x - x tan² 30° 1 + tan² 30°
= sin²30° + 4 cot²45° – sec²60°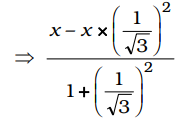
= 
1 
² + 4 × (1)² - (2)² 2 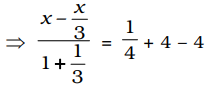
⇒ 3x - x = 1 3 + 1 4 ⇒ 2x = 1 × 4 = 1 4 ⇒ x = 1 2
- If cos θ + sin θ = m and sec θ + cosec θ = n then the value of n (m² – 1) is equal to :
-
View Hint View Answer Discuss in Forum
cosθ + sinθ = m --- (i)
secθ + cosecθ = n⇒ 1 + 1 = n cosθ sinθ ⇒ sinθ + cosθ = n --- (ii) sinθ . cosθ ∴ n (m² – 1) = sinθ + cosθ sinθ . cosθ
[(sinθ + cosθ)² – 1]= sinθ + cosθ (sin²θ + cos²θ + 2sinθ cosθ – 1) sinθ . cosθ = sinθ + cosθ × 2sinθ . cosθ sinθ . cosθ
[∵sin²θ + cos²θ = 1]
= 2 (sinθ + cosθ) = 2mCorrect Option: A
cosθ + sinθ = m --- (i)
secθ + cosecθ = n⇒ 1 + 1 = n cosθ sinθ ⇒ sinθ + cosθ = n --- (ii) sinθ . cosθ ∴ n (m² – 1) = sinθ + cosθ sinθ . cosθ
[(sinθ + cosθ)² – 1]= sinθ + cosθ (sin²θ + cos²θ + 2sinθ cosθ – 1) sinθ . cosθ = sinθ + cosθ × 2sinθ . cosθ sinθ . cosθ
[∵sin²θ + cos²θ = 1]
= 2 (sinθ + cosθ) = 2m
- If x = a (sin θ + cos θ) and y = b (sin θ – cos θ), then the value of
x² + y² is : a² b²
-
View Hint View Answer Discuss in Forum
x = a (sinθ + cosθ)
⇒ x = sinθ + cosθ a
and, y = b (sinθ – cosθ)⇒ y = sinθ - cosθ b ∴ x² + y² a² b²
= (sinθ + cosθ)² + (sinθ – cosθ)² = 2 (sin²θ + cos²θ) = 2 [∵ (a + b)² + (a – b)² = 2 (a² + b² )]
Correct Option: D
x = a (sinθ + cosθ)
⇒ x = sinθ + cosθ a
and, y = b (sinθ – cosθ)⇒ y = sinθ - cosθ b ∴ x² + y² a² b²
= (sinθ + cosθ)² + (sinθ – cosθ)² = 2 (sin²θ + cos²θ) = 2 [∵ (a + b)² + (a – b)² = 2 (a² + b² )]
- The value of the expression sin²1° + sin²11° + sin²21° + sin²31° + sin²41° + sin²45° + sin²49° + sin²59° + sin²69° + sin²79° + sin²89° is :
-
View Hint View Answer Discuss in Forum
sin 89° = sin (90°–1°) = cos 1°
sin 79° = sin (90°–11°) = cos 11°
sin 69° = sin (90°–21°) = cos 21°
sin 59° = sin (90°–31°) = cos 31°
sin 49° = sin (90°–41°) = cos 41°
∴ Expression
= (sin²1° + cos²1°) + (sin²11° + cos²11°) + (sin²21° + cos²21°) + (sin²31° + cos²31°) + (sin²41° + cos²41°) + sin²45°
[∵ sin²θ + cos²θ = 1]Correct Option: B
sin 89° = sin (90°–1°) = cos 1°
sin 79° = sin (90°–11°) = cos 11°
sin 69° = sin (90°–21°) = cos 21°
sin 59° = sin (90°–31°) = cos 31°
sin 49° = sin (90°–41°) = cos 41°
∴ Expression
= (sin²1° + cos²1°) + (sin²11° + cos²11°) + (sin²21° + cos²21°) + (sin²31° + cos²31°) + (sin²41° + cos²41°) + sin²45°
[∵ sin²θ + cos²θ = 1]
- If the elevation of the Sun changes from 30° to 60°, then the difference between the lengths of shadows of a pole 15 metre high, is
-
View Hint View Answer Discuss in Forum
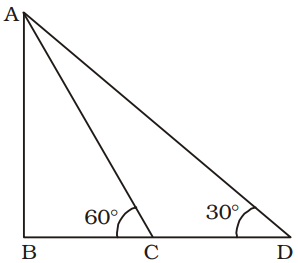
AB = Height of pole = 15 metre
∠ACB = 60°; ∠ADB = 30°
In ∆ABC,tan 60° = AB ⇒ √3 = 15 BC BC ⇒ BC = 15 = 5√3 metre √3
In ∆ABD,tan 30° = AB BD ⇒ 1 = 15 √3 BD
⇒ BD = 15 √3 metre
∴ Required difference
= BD – BC = (15√3 - 5√3) metre
= 10 √3 metreCorrect Option: C

AB = Height of pole = 15 metre
∠ACB = 60°; ∠ADB = 30°
In ∆ABC,tan 60° = AB ⇒ √3 = 15 BC BC ⇒ BC = 15 = 5√3 metre √3
In ∆ABD,tan 30° = AB BD ⇒ 1 = 15 √3 BD
⇒ BD = 15 √3 metre
∴ Required difference
= BD – BC = (15√3 - 5√3) metre
= 10 √3 metre

