81. The numerical value of		5	+	2	+ 3 sinsec² θ is:
    		sec² θ		1 + cot² θ

1. 1. 5

   
   
   

   2. 2

   
   
   

   3. 3

   
   
   

   4. 4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Expression
   

   =		5	+	2	+ 3sin²θ
   		sec²θ		1 + cot²θ

   
   

   = 5cos² θ +	2	+ 3² θ
   	cosec² θ

   
   = 5 cos²θ + 2 sin²θ + 3 sin²θ
   = 5 (cos²θ + sin²θ) = 5
   
   

   Correct Option: A

   Expression
   

   =		5	+	2	+ 3sin²θ
   		sec²θ		1 + cot²θ

   
   

   = 5cos² θ +	2	+ 3² θ
   	cosec² θ

   
   = 5 cos²θ + 2 sin²θ + 3 sin²θ
   = 5 (cos²θ + sin²θ) = 5
   
   

---

82. If cos θ + secθ = 2, the value of cos⁶θ + sec⁶θ is

1. 1. 4

   
   
   

   2. 8

   
   
   

   3. 1

   
   
   

   4. 2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   cosθ + secθ = 2
   

   ⇒ cos θ +	1	= 2
   	cos θ

   
   ⇒ cos²θ – 2 cosθ + 1 = 0
   ⇒ (cosθ – 1)² = 0
   ⇒ cosθ = 1
   ⇒ secθ = 1
   ∴ cos⁶θ + sec⁶θ = 1 + 1 = 2

   Correct Option: D

   cosθ + secθ = 2
   

   ⇒ cos θ +	1	= 2
   	cos θ

   
   ⇒ cos²θ – 2 cosθ + 1 = 0
   ⇒ (cosθ – 1)² = 0
   ⇒ cosθ = 1
   ⇒ secθ = 1
   ∴ cos⁶θ + sec⁶θ = 1 + 1 = 2

---

---

83. If 2 sin (πx / 2) = x² + (1 / x²) , then the value of [x - (1 / x)] is

1. 1. - 1

   
   
   

   2. 2

   
   
   

   3. 1

   
   
   

   4. 0

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

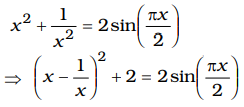
   ⇒ x -	1	= 0 [∵ sin θ ≤ 1]
   	x

   
   

   Correct Option: D

   
   

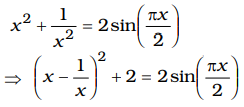
   ⇒ x -	1	= 0 [∵ sin θ ≤ 1]
   	x

   
   

---

84. The minimum value of sin²θ + cos²θ + sec²θ + cosec²θ + tan²θ + cot²θ is
    

1. 1. 1

   
   
   

   2. 3

   
   
   

   3. 5

   
   
   

   4. 7

   
   
   

---

1. View Hint View Answer Discuss in Forum

   sin²θ + cos²θ + sec²θ + cosec²θ + tan²θ + cot²θ
   = 1 + sec²θ – tan²θ + cosec²θ – cot²θ + 2(tan²θ + cot²θ )
   = 3 + 2 ((tanθ – cotθ) ² + 2) > 7
   [(tanθ – cotθ) ² > 0]

   Correct Option: D

   sin²θ + cos²θ + sec²θ + cosec²θ + tan²θ + cot²θ
   = 1 + sec²θ – tan²θ + cosec²θ – cot²θ + 2(tan²θ + cot²θ )
   = 3 + 2 ((tanθ – cotθ) ² + 2) > 7
   [(tanθ – cotθ) ² > 0]

---

---

85. In a right-angled triangle XYZ, right-angled at Y, if XY = 2 √6 and XZ – YZ = 2, then sec X + tan X is

1. 1. -	1
      	√6

   
   
   

   2. √6

   
   
   

   3. 2√6

   
   
   

   4. -	√6
      	2

      
      

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
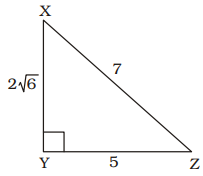
   XZ – YZ = 2 .... (i)
   ⇒ XY² + YZ² = XZ²
   ⇒ ⇒ (2√6)² XZ² - YZ²
   ⇒ 24 = (XZ – YZ) (XZ + YZ)
   ⇒ XZ +YZ = 12 ....(ii)
   Adding both the equations,
   2 X Z = 14 ⇒ XZ = 7
   ∴ YZ = 7 – 2 = 5
   

   ∴ sec X =	7
   	2√6

   
   

   & tan X =	5
   	2√6

   
   

   ∴ sec X + tanX =		7	+	5
   		2√6		2√6

   
   

   =	12	= √6
   	2√6

   
   

   Correct Option: B

   
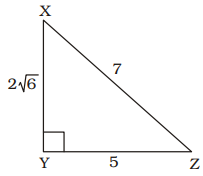
   XZ – YZ = 2 .... (i)
   ⇒ XY² + YZ² = XZ²
   ⇒ ⇒ (2√6)² XZ² - YZ²
   ⇒ 24 = (XZ – YZ) (XZ + YZ)
   ⇒ XZ +YZ = 12 ....(ii)
   Adding both the equations,
   2 X Z = 14 ⇒ XZ = 7
   ∴ YZ = 7 – 2 = 5
   

   ∴ sec X =	7
   	2√6

   
   

   & tan X =	5
   	2√6

   
   

   ∴ sec X + tanX =		7	+	5
   		2√6		2√6

   
   

   =	12	= √6
   	2√6

   
   

---