496. If   y = 2secθ and x = 3 tanθ then	x2	−	y2	is
     	9		4

1. 1. 0

   
   
   

   2. –1

   
   
   

   3. 2

   
   
   

   4. 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   y = 2secθ ⇒ secθ =	y
   	2

   
   

   and x = 3 tanθ ⇒ tanθ =	x
   	3

   
   ∵  sec²θ – tan²θ = 1
   

   ⇒	y2	−	x2	= 1
   	4		9

   
   

   ⇒	x2	−	y2	= 1
   	9		4

   Correct Option: B

   y = 2secθ ⇒ secθ =	y
   	2

   
   

   and x = 3 tanθ ⇒ tanθ =	x
   	3

   
   ∵  sec²θ – tan²θ = 1
   

   ⇒	y2	−	x2	= 1
   	4		9

   
   

   ⇒	x2	−	y2	= 1
   	9		4

---

497. If	cosecθ + sinθ	=	5	then the value of sinq is equal to
     	cosecθ − sinθ		3

1. 1. 1

      2

   
   
   

   2. 1

      √2

   
   
   

   3. √3

      2

   
   
   

   4. 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   cosecθ + sinθ	=	5
   cosecθ − sinθ		3

   
   ⇒  5 cosecθ – 5 sinθ
   = 3 cosecθ + 3 sinθ
   ⇒  5 cosecθ – 3 cosecθ
   = 5 sinθ + 3 sinθ
   ⇒  2 cosecθ = 8 sinθ
   

   ⇒	1	= 4 sinθ
   	sinθ

   
   ⇒  4 sin²θ = 1 ⇒ 2sinθ = 1
   

   ⇒  sinθ =	1
   	2

   Correct Option: A

   cosecθ + sinθ	=	5
   cosecθ − sinθ		3

   
   ⇒  5 cosecθ – 5 sinθ
   = 3 cosecθ + 3 sinθ
   ⇒  5 cosecθ – 3 cosecθ
   = 5 sinθ + 3 sinθ
   ⇒  2 cosecθ = 8 sinθ
   

   ⇒	1	= 4 sinθ
   	sinθ

   
   ⇒  4 sin²θ = 1 ⇒ 2sinθ = 1
   

   ⇒  sinθ =	1
   	2

---

---

498. If sinθ =	√3	and 0° < θ < 90°, then the value of tan (θ – 15°) is
     	2

1. 1. 1

   
   
   

   2. √3

   
   
   

   3. 1

      √3

   
   
   

   4. √2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   sinθ =	√3	= sin60°
   	2

   
   ⇒  θ = 60°
   ∴  tan (θ – 15°)
   = tan (60° – 15°) = tan 45° = 1

   Correct Option: A

   sinθ =	√3	= sin60°
   	2

   
   ⇒  θ = 60°
   ∴  tan (θ – 15°)
   = tan (60° – 15°) = tan 45° = 1

---

499. If the angle of elevation of the Sun changes from 30° to 45°, the length of the shadow of a pillar decreases by 20 metres. The height of the pillar is

1. 1. 20 ( √3 –1) m

   
   
   

   2. 20 ( √3 + 1) m

   
   
   

   3. 10 ( √3 –1) m

   
   
   

   4. 10 ( √3 +1) m

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
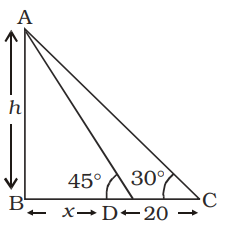
   Let AB be a pillar of height h meter
   If BD = length of shadow = x
   and DC = 20 m
   then, BC = BD + DC
   ⇒ BC = (x + 20) metre
   From ∆ ABD,
   

   tan 45° =	h	⇒ h = x ...(i)
   	x

   
   From ∆ ABC,
   

   tan30° =	AB	⇒	1	=	h
   	BC		√3		x + 20

   
   

   ⇒	1	=	h	⇒ √3h = h + 20
   	√3		x + 20

   
   [From (i)]
   

   ⇒ (√3 - 1)h = 20 ⇒ h =	h
   	√3 - 1

   
   

   =	20	×	√3 + 1
   	√3 - 1		√3 + 1

   
   

   =	20(√3 + 1)	= 10(√3 + 1) metre
   	2

   Correct Option: D

   
   Let AB be a pillar of height h meter
   If BD = length of shadow = x
   and DC = 20 m
   then, BC = BD + DC
   ⇒ BC = (x + 20) metre
   From ∆ ABD,
   

   tan 45° =	h	⇒ h = x ...(i)
   	x

   
   From ∆ ABC,
   

   tan30° =	AB	⇒	1	=	h
   	BC		√3		x + 20

   
   

   ⇒	1	=	h	⇒ √3h = h + 20
   	√3		x + 20

   
   [From (i)]
   

   ⇒ (√3 - 1)h = 20 ⇒ h =	h
   	√3 - 1

   
   

   =	20	×	√3 + 1
   	√3 - 1		√3 + 1

   
   

   =	20(√3 + 1)	= 10(√3 + 1) metre
   	2

---

---

500. The value of (1 + tan²θ) (1 – sin²θ)

1. 1. 2

   
   
   

   2. 1

   
   
   

   3. –1

   
   
   

   4. –2

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Expression
   = (1 + tan²θ) .(1 – sin²θ)
   = sec²θ . cos²θ = 1
   [∵  sec²θ – tan²θ = 1 = sin²θ + cos²θ ; secθ . cosθ = 1]

   Correct Option: B

   Expression
   = (1 + tan²θ) .(1 – sin²θ)
   = sec²θ . cos²θ = 1
   [∵  sec²θ – tan²θ = 1 = sin²θ + cos²θ ; secθ . cosθ = 1]

---