-
If the angle of elevation of the Sun changes from 30° to 45°, the length of the shadow of a pillar decreases by 20 metres. The height of the pillar is
-
- 20 ( √3 –1) m
- 20 ( √3 + 1) m
- 10 ( √3 –1) m
- 10 ( √3 +1) m
Correct Option: D
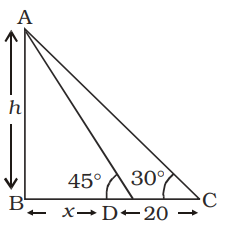
Let AB be a pillar of height h meter
If BD = length of shadow = x
and DC = 20 m
then, BC = BD + DC
⇒ BC = (x + 20) metre
From ∆ ABD,
| tan 45° = | ⇒ h = x ...(i) | x |
From ∆ ABC,
| tan30° = | ⇒ | = | ||||
| BC | √3 | x + 20 |
| ⇒ | = | ⇒ √3h = h + 20 | ||
| √3 | x + 20 |
[From (i)]
| ⇒ (√3 - 1)h = 20 ⇒ h = | √3 - 1 |
| = | × | |||
| √3 - 1 | √3 + 1 |
| = | = 10(√3 + 1) metre | 2 |

