Trigonometry
-
If x - tan²30° = sin²30° + 4 cot² 45° – sec² 60°, then the value of x is : 1 + tan²30°
-
View Hint View Answer Discuss in Forum
x - x tan² 30° 1 + tan² 30°
= sin²30° + 4 cot²45° – sec²60°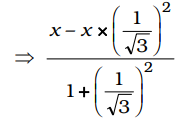
= 
1 
² + 4 × (1)² - (2)² 2 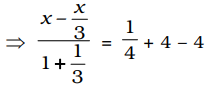
⇒ 3x - x = 1 3 + 1 4 ⇒ 2x = 1 × 4 = 1 4 ⇒ x = 1 2
Correct Option: C
x - x tan² 30° 1 + tan² 30°
= sin²30° + 4 cot²45° – sec²60°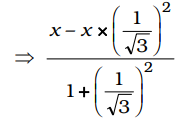
= 
1 
² + 4 × (1)² - (2)² 2 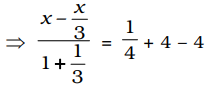
⇒ 3x - x = 1 3 + 1 4 ⇒ 2x = 1 × 4 = 1 4 ⇒ x = 1 2
- If cos A + sin A = √2 cos A then cos A – sin A is equal to : (where 0° < A < 90°)
-
View Hint View Answer Discuss in Forum
cosA + sinA = 2 cosA --- (i)
cosA – sinA = x (let) --- (ii)
On squaring both equation and adding
cos²A + sin²A + 2 sinA . cosA + cos²A + sin²A – 2 sinA cosA = 2
cos²A + x ²
⇒ 2 (cos²A + sin²A) = 2 cos²A + x 2
⇒ x² + 2 cos²A = 2
⇒ x² = 2 – 2 cos²A
= 2 (1 – cos²A) = 2 sin²A
∴ x = √2 sin ACorrect Option: A
cosA + sinA = 2 cosA --- (i)
cosA – sinA = x (let) --- (ii)
On squaring both equation and adding
cos²A + sin²A + 2 sinA . cosA + cos²A + sin²A – 2 sinA cosA = 2
cos²A + x ²
⇒ 2 (cos²A + sin²A) = 2 cos²A + x 2
⇒ x² + 2 cos²A = 2
⇒ x² = 2 – 2 cos²A
= 2 (1 – cos²A) = 2 sin²A
∴ x = √2 sin A
-
If sin θ + cosθ = 3 then the value of sin4 q is : sin θ - cosθ
-
View Hint View Answer Discuss in Forum
sinθ + cosθ = 3 sinθ - cosθ 1
By componendo and dividendosin θ + cos θ + sin θ – cosθ = 3 + 1 sin θ + cos θ - sin θ + cosθ 3 - 1 ⇒ 2 sinθ = 4 2 cosθ 2
⇒ tanθ = 2∴ cotθ = 1 2
∴ cosecθ = √1 + cot² θ
∴ sin θ = 2 √5 sin4θ = 16 25
Correct Option: E
sinθ + cosθ = 3 sinθ - cosθ 1
By componendo and dividendosin θ + cos θ + sin θ – cosθ = 3 + 1 sin θ + cos θ - sin θ + cosθ 3 - 1 ⇒ 2 sinθ = 4 2 cosθ 2
⇒ tanθ = 2∴ cotθ = 1 2
∴ cosecθ = √1 + cot² θ
∴ sin θ = 2 √5 sin4θ = 16 25
- The angle of elevation of an aeroplane from a point on the ground is 45°. After flying for 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 2500 metres, then the speed of the aeroplane in km/ hr. is
-
View Hint View Answer Discuss in Forum

Let A and C be the positions of plane.
AB = CD = 2500 metre
BD = AC = x metre (let)
∠AOB = 60° ; ∠COD = 30°
In ∆OAB,
⇒ OB = 2500 metre
In ∆OCD,tan30° = CD OD ⇒ 1 √3 = 2500 2500 + x
⇒ 2500 + x = 2500√3
⇒ x
= 2500 √3 – 2500
= 2500 (√3 - 1) metre
Time = 15 seconds= 15 hour = 1 hour 60 × 60 240 ∴ Speed of plane = 2500 (√3 - 1) × 240 kmph 1000
= 600 (√3 - 1) kmph.Correct Option: D

Let A and C be the positions of plane.
AB = CD = 2500 metre
BD = AC = x metre (let)
∠AOB = 60° ; ∠COD = 30°
In ∆OAB,
⇒ OB = 2500 metre
In ∆OCD,tan30° = CD OD ⇒ 1 √3 = 2500 2500 + x
⇒ 2500 + x = 2500√3
⇒ x
= 2500 √3 – 2500
= 2500 (√3 - 1) metre
Time = 15 seconds= 15 hour = 1 hour 60 × 60 240 ∴ Speed of plane = 2500 (√3 - 1) × 240 kmph 1000
= 600 (√3 - 1) kmph.
- A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angle of elevation of the bottom of the flag staff is a and that of the top of the flag staff is β. Then the height of the tower is
-
View Hint View Answer Discuss in Forum

Let height of tower = BC = y metre
AB = height of flag-staff = h metre
∠BDC = a; ∠ADC = b
Let, CD = x metre
In ∆BCD,tan α = BC CD ⇒ tan α = y ..... (i) x
In ∆ACD,tan β = AC CD ⇒ tan β = h + y x ⇒ x = h + y ..... (ii) tanβ ∴ y = h + y tanα tanβ
⇒ y tan β = h tanα + y tanα
⇒ y tanβ – y tanα = h tanα
⇒ y (tanβ – tanα) = h tanα⇒ y = h tan α tanβ - tanα
Correct Option: B

Let height of tower = BC = y metre
AB = height of flag-staff = h metre
∠BDC = a; ∠ADC = b
Let, CD = x metre
In ∆BCD,tan α = BC CD ⇒ tan α = y ..... (i) x
In ∆ACD,tan β = AC CD ⇒ tan β = h + y x ⇒ x = h + y ..... (ii) tanβ ∴ y = h + y tanα tanβ
⇒ y tan β = h tanα + y tanα
⇒ y tanβ – y tanα = h tanα
⇒ y (tanβ – tanα) = h tanα⇒ y = h tan α tanβ - tanα

