Trigonometry
- A man standing on the bank of a river observes that the angle of elevation of the top of a tree just on the opposite bank is 60°. But angle of elevation is 30° from a point which is at a distance 20 √3 ft away from the bank. Then the height of the tree is :
-
View Hint View Answer Discuss in Forum

Suppose, height of tree = AB = h foot
BC = width of river = x foot
CD = 20 3 foot
∠ACB = 60° and ∠ADB = 30°
In ∆ABC,tan60° = AB BC ⇒ √3 = h x
⇒ h = √3x foot ...............(i)
In ∆ABD,tan30° = AB BD = 1 = h √3 x + 20√3
⇒ √3h x = + 20 √3⇒ √3h = h + 20√3 √3
⇒ 3h = h + 20 √3 × √3
⇒ 2h = 60⇒ h = 60 = 30 feet 2
Correct Option: C

Suppose, height of tree = AB = h foot
BC = width of river = x foot
CD = 20 3 foot
∠ACB = 60° and ∠ADB = 30°
In ∆ABC,tan60° = AB BC ⇒ √3 = h x
⇒ h = √3x foot ...............(i)
In ∆ABD,tan30° = AB BD = 1 = h √3 x + 20√3
⇒ √3h x = + 20 √3⇒ √3h = h + 20√3 √3
⇒ 3h = h + 20 √3 × √3
⇒ 2h = 60⇒ h = 60 = 30 feet 2
- The length of shadow of a tower is √3 times that of its length. The angle of elevation of the sun is :
-
View Hint View Answer Discuss in Forum
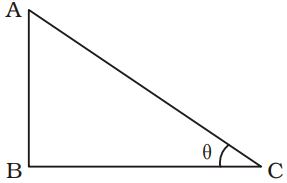
Let the height of tower be x units.
∴ Length of shadow = √3x units In ∆ABC,∴ tanθ = AB = x = 1 BC √3 x √3
⇒ tanθ = tan30°
⇒ θ = 30°Correct Option: B

Let the height of tower be x units.
∴ Length of shadow = √3x units In ∆ABC,∴ tanθ = AB = x = 1 BC √3 x √3
⇒ tanθ = tan30°
⇒ θ = 30°
- From the top of a 20 metre high building, the angle of elevation of the top of a tower is 60° and the angle of depression of its foot is at 45°, then the height of the tower is (√3 = 1.732)
-
View Hint View Answer Discuss in Forum

AB = Height of building = 20 metre
CD = Height of tower = h metre (let)
∠ACB = ∠EAC = 45°
∠DAE = 60°
BC = AE = x metre
In ∆ABC,tan 45° = AB BC ⇒ 1 = 20 x
⇒ x = 20 metre
In ∆ADE,tan 60° = DE ⇒ √3 = h - 20 AE 20
&RArr; h – 20 = 20√3
⇒ h = 20√3 + 20
= 20(√3 + 1)metre
= 20 (1.732 + 1) metre
= (20 × 2.732) metre
= 54.64 metre
Correct Option: C

AB = Height of building = 20 metre
CD = Height of tower = h metre (let)
∠ACB = ∠EAC = 45°
∠DAE = 60°
BC = AE = x metre
In ∆ABC,tan 45° = AB BC ⇒ 1 = 20 x
⇒ x = 20 metre
In ∆ADE,tan 60° = DE ⇒ √3 = h - 20 AE 20
&RArr; h – 20 = 20√3
⇒ h = 20√3 + 20
= 20(√3 + 1)metre
= 20 (1.732 + 1) metre
= (20 × 2.732) metre
= 54.64 metre
- Two persons are on either side of a temple, 75 m high, observe the angle of elevation of the top of the temple to be 30° and 60° respectively. The distance between the persons is :
-
View Hint View Answer Discuss in Forum

AD = Height of temple = 75 metre
B and C ⇒ Positions of men
∠ABD = 30°; ∠ACD = 60°
In ∆ABD,tan 30° = AD BD ⇒ 1 = 75 √3 BD
⇒ BD = 75 √3 metre
In ∆ACD,tan 60° = AD DC ⇒ √3 = 75 DC ⇒ DC = 75 = 25√3 metre √3
∴ BC = BD + DC
= 75 √3 + 25 √3
= 100 √3 metre
= (100 × 1.732) metre
= 173.2 metreCorrect Option: A

AD = Height of temple = 75 metre
B and C ⇒ Positions of men
∠ABD = 30°; ∠ACD = 60°
In ∆ABD,tan 30° = AD BD ⇒ 1 = 75 √3 BD
⇒ BD = 75 √3 metre
In ∆ACD,tan 60° = AD DC ⇒ √3 = 75 DC ⇒ DC = 75 = 25√3 metre √3
∴ BC = BD + DC
= 75 √3 + 25 √3
= 100 √3 metre
= (100 × 1.732) metre
= 173.2 metre
- The angles of elevation of an aeroplane flying vertically above the ground, as observed from the two consecutive stones, 1 km apart; are 45° and 60° aeroplane from the ground is :
-
View Hint View Answer Discuss in Forum

Two consecutive kilometre stones ⇒ C and D
∠ADB = 45°; ∠ACB = 60°
CD = 1 km.
AB = height of plane = h metre
BC = x metre (let)
In ∆ABC,tan60° = AB BC ⇒ √3 = h x
⇒ h = √3x metre ..... (i)
In ∆ABDtan45° = AB BD ⇒ 1 = h x + 1
⇒ h = x + 1⇒ h = h + 1 √3
[From equation (i)]⇒ h - h = 1 √3 ⇒ √3h - h = 1 √3
⇒ (√3 - 1)h = √3⇒ h = √3 √3 - 1 ⇒ h = √3(√3 + 1) (√3 - 1)(√3 + 1) ⇒ h = √3(√3 + 1) 2 h = (3 + √3) metre 2
Correct Option: D

Two consecutive kilometre stones ⇒ C and D
∠ADB = 45°; ∠ACB = 60°
CD = 1 km.
AB = height of plane = h metre
BC = x metre (let)
In ∆ABC,tan60° = AB BC ⇒ √3 = h x
⇒ h = √3x metre ..... (i)
In ∆ABDtan45° = AB BD ⇒ 1 = h x + 1
⇒ h = x + 1⇒ h = h + 1 √3
[From equation (i)]⇒ h - h = 1 √3 ⇒ √3h - h = 1 √3
⇒ (√3 - 1)h = √3⇒ h = √3 √3 - 1 ⇒ h = √3(√3 + 1) (√3 - 1)(√3 + 1) ⇒ h = √3(√3 + 1) 2 h = (3 + √3) metre 2

