-
If the angle of elevation of the top of a pillar from the ground level is raised from 30° to 60°, the length of the shadow of a pillar of height 50 √3 will be decreased by
-
- 60 metre
- 75 metre
- 100 metre
- 50 metre
Correct Option: C
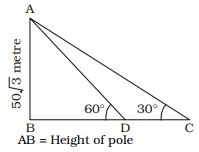
AB = Height of pole = 50 √3 metre
BC = Length of shadow = x metre
When, ∠ACB = 30°
BD = Length of shadow = y metre
when, ∠ADB = 60°
In ∆ABC,
| tan30° = | ||
| BC |
| ⇒ | = | ||
| √3 | x |
⇒ x = 50√3 × √3 = 150 metre
In ∆ABD
| tan60° = | ||
| BD |
| ⇒ √3 = | ||
| y |
| ⇒ y = | = 50 metre | |
| √3 |
∴ CD = x – y = 150 – 50 = 100 metre

