From an aeroplane just over a straight road, the angles

Home » Aptitude » Trigonometry » Question

From an aeroplane just over a straight road, the angles of depression of two consecutive kilometre stones situated at opposite sides of the aeroplane were found to be 60° and 30° respectively. The height (in km) of the aeroplane from the road at that instant was (Given √3 = 1.732)

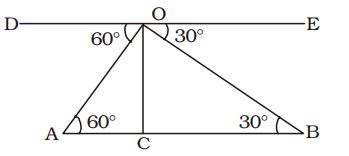
OC = Height of plane = h km (let)
∠DOA = ∠OAC = 60° ;
∠BOE = ∠OBC = 30°
AB = 2 km.
AC = x km (let)
∴ BC = (2 – x ) km.
From, ∆OAC

tan 60° =	OC
	AC

⇒ √3 =	h
	x

⇒ x = =	h	km. ...(i)
	√3

From ∆OBC,

tan 30° =	OC
	CB

⇒	1	=	h
	√3		2 - x

⇒√3 h = 2 –	h	[From equation(i)]
	√3

[From equation(i)]

⇒√3 h +	h	= 2
	√3

⇒	3h + h	= 2
	√3

⇒ 4h = 2 √3

⇒ h =	2√3	=	√3	km.
	4		2

=	1.732	= 0.866 km.
	2