Plane Geometry
- From the circumcentre I of the triangle ABC, perpendicular ID is drawn on BC. If ∠BAC = 60°, then the value of ∠BID is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a triangle ABC
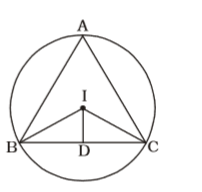
Here , ∠BAC = 60°
BI = IC = in–radius
∴ Angle subtended by arc AC at the centre = 2 × ∠BAC
Angle subtended by arc AC at the centre = 2 × 60° = 120°Correct Option: A
As per the given in question , we draw a figure of a triangle ABC

Here , ∠BAC = 60°
BI = IC = in–radius
∴ Angle subtended by arc AC at the centre = 2 × ∠BAC
Angle subtended by arc AC at the centre = 2 × 60° = 120°∴ ∠BID = ∠DIC = 120° = 60° 2
- O is the circumcentre of a triangle ∆ ABC. The point A and th chord BC are on the opposite side of O. If ∠BOC = 150°. Then the angle ∠BAC is :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of triangle ABC circumscribes a circle with centre O
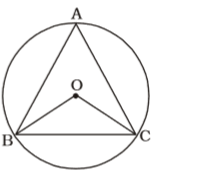
Given , ∠BOC = 150°
As we know that Angle subtended at the centre of a circled by an arc is twice to that at the circumference.
∴ ∠BOC = 2∠BACCorrect Option: D
According to question , we draw a figure of triangle ABC circumscribes a circle with centre O

Given , ∠BOC = 150°
As we know that Angle subtended at the centre of a circled by an arc is twice to that at the circumference.
∴ ∠BOC = 2∠BAC⇒ ∠BAC = 150 = 75° 2
- The circumcentre of a triangle ABC is O. If ∠BAC = 85°, ∠BCA = 75°, then ∠OAC is of
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a a triangle ABC whose circumcentre is O ,
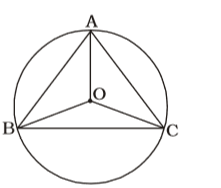
Point ‘O’ is equidistant from the vertices of triangle ABC.
∴ OA = OB = OC
∴ ∠OAC = ∠OCA, ∠OBC = ∠OCB; ∠OAB = ∠OBA
∴ In ∆ ABC,
∠ABC = 180° – 85° – 75° = 20°
∴ ∠AOC = 2 ∠ABC = 2 × 20° = 40°
∴ In ∆ AOC,
2 ∠OAC + 40° = 180°Correct Option: A
On the basis of question we draw a figure of a a triangle ABC whose circumcentre is O ,

Point ‘O’ is equidistant from the vertices of triangle ABC.
∴ OA = OB = OC
∴ ∠OAC = ∠OCA, ∠OBC = ∠OCB; ∠OAB = ∠OBA
∴ In ∆ ABC,
∠ABC = 180° – 85° – 75° = 20°
∴ ∠AOC = 2 ∠ABC = 2 × 20° = 40°
∴ In ∆ AOC,
2 ∠OAC + 40° = 180°
⇒ 2 ∠OAC = 180° – 40° = 140°⇒ ∠OAC = 140° = 70° 2
- The ratio of inradius and circumradius of an equilateral triangle is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of an equilateral triangle with inradius and circumradius
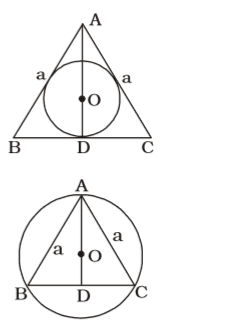
As we know that ,AD = √3 × Side 2 ∴ OD = 1 × AD √3 OD = 1 × √3a = a 3 2 2√3 OA = 2 AD 3 OA = 2 × √3 a = a 3 2 √3 In-radius = Side = a 2√3 2√3
Correct Option: A
As per the given in question , we draw a figure of an equilateral triangle with inradius and circumradius

As we know that ,AD = √3 × Side 2 ∴ OD = 1 × AD √3 OD = 1 × √3a = a 3 2 2√3 OA = 2 AD 3 OA = 2 × √3 a = a 3 2 √3 In-radius = Side = a 2√3 2√3 Circum-radius = Side = a √3 √3 ∴ Required ratio = a : a = 1 : 2 2√3 √3
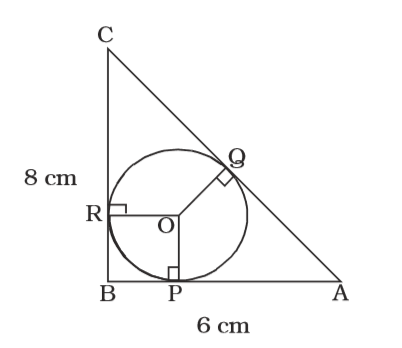
- ∆ ABC is a right angled triangle with AB = 6 cm, BC = 8 cm. O is the incentre of the triangle. The radius of the in-circle is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a right angled triangle ABC and O is the incentre of the triangle
Given , AB = 6 cm, BC = 8 cm
OP = OQ = OR = r (let)
∠CBA = 90°
From ∆ABC ,
∴ AC = √AB² + BC²
AC = √6² + 8² = √36 + 64
AC = √100 = 10 cm.
Area of ∆ ABC = Area of ( ∆ AOC + ∆ BOC + ∆ AOB)⇒ 1 × 6 × 8 = 1 × AC × OQ + 1 × BC × OR + 1 × AB × OP 2 2 2 2
Correct Option: C
As per the given in question , we draw a figure of a right angled triangle ABC and O is the incentre of the triangle

Given , AB = 6 cm, BC = 8 cm
OP = OQ = OR = r (let)
∠CBA = 90°
From ∆ABC ,
∴ AC = √AB² + BC²
AC = √6² + 8² = √36 + 64
AC = √100 = 10 cm.
Area of ∆ ABC = Area of ( ∆ AOC + ∆ BOC + ∆ AOB)⇒ 1 × 6 × 8 = 1 × AC × OQ + 1 × BC × OR + 1 × AB × OP 2 2 2 2 ⇒ 24 = 1 × 10 × r + 1 × 8 × r + 1 × 6 × r 2 2 2
⇒ 24 = 5r + 4r + 3r⇒ 12r = 24 ⇒ r = 24 = 2 cm. 2

