As per the given in question , we draw a figure a circle,

Given , OC = 3 cm
OA = 5 cm
AC = √OA² - OC²

Correct Option: D

As per the given in question , we draw a figure a circle,

Given , OC = 3 cm
OA = 5 cm
AC = √OA² - OC²
AC = √5² - 3² = 4
∴ AB = 2AC = 8 cm

According to question , we draw a figure of a circle ,

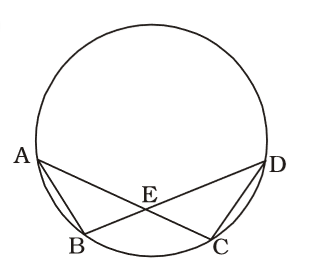
Given, ∠BEC = 130° and ∠ECD = 20°
⇒ ∠DEC = 180° – 130° = 50°

Correct Option: D

According to question , we draw a figure of a circle ,

Given, ∠BEC = 130° and ∠ECD = 20°
⇒ ∠DEC = 180° – 130° = 50°
∴ ∠EDC = 180° – 50° – 20° = 110°
∴ ∠BAC = ∠EDC = 110°
(Angles on the same arc)

According to question , we draw a figure of a circle with centre O ,

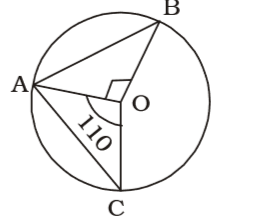
[∵ BOC is not a straight line]
From figure , ∠AOB = 90° ; OA = OB = r
∴ ∠BAO = ∠ABO = 45°
∴ ∠AOC = 110° ; OA = OC = r

Correct Option: B

According to question , we draw a figure of a circle with centre O ,

[∵ BOC is not a straight line]
From figure , ∠AOB = 90° ; OA = OB = r
∴ ∠BAO = ∠ABO = 45°
∴ ∠AOC = 110° ; OA = OC = r

n the basis of question we draw a figure of a two circles touch each other externally ,

Given , OƠ = 7 cm
We know that ,
OƠ = r₁ + r₂
⇒ r₁ + r₂ = 7

Correct Option: B

n the basis of question we draw a figure of a two circles touch each other externally ,

Given , OƠ = 7 cm
We know that ,
OƠ = r₁ + r₂
⇒ r₁ + r₂ = 7
⇒ 4 + r₂ = 7
⇒ r₂ = 7 – 4 = 3 cm

According to question , we draw a figure of two circles touch each other internally ,

Given , ƠA = 3 cm and OA = 2 cm
CA = 6 cm
ƠD = 3 cm
ƠB = 1 cm

Correct Option: D

According to question , we draw a figure of two circles touch each other internally ,

Given , ƠA = 3 cm and OA = 2 cm
CA = 6 cm
ƠD = 3 cm
ƠB = 1 cm
BD = √3² - 1 = 2√2
∴ DE = 4√2 cm