As per the given in question , we draw a figure cyclic trapezium ABCD

As we know that the sum of the opposite angles of a concyclic quadrilateral is 180°.
∴ ∠ABC + ∠ADC = 180°
⇒ 70° + ∠ADC = 180°
⇒ ∠ADC = 180° – 70° = 110°
∵ AD || BC
∴ ∠ADC + ∠BCD = 180°

Correct Option: C

As per the given in question , we draw a figure cyclic trapezium ABCD

As we know that the sum of the opposite angles of a concyclic quadrilateral is 180°.
∴ ∠ABC + ∠ADC = 180°
⇒ 70° + ∠ADC = 180°
⇒ ∠ADC = 180° – 70° = 110°
∵ AD || BC
∴ ∠ADC + ∠BCD = 180°
⇒ 110° + ∠BCD = 180°
⇒ ∠BCD = 180° – 110° = 70°.

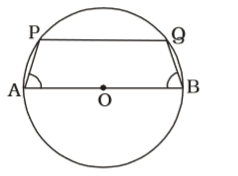
AB is a diameter of a circle having centre at O. PQ is a chord which does not intersect AB ,

Correct Option: B

AB is a diameter of a circle having centre at O. PQ is a chord which does not intersect AB ,

∠PAB = ∠ABQ
∴ PQ || AB

According to question , we draw a figure of rhombus ABCD in which AC is its smallest diagonal

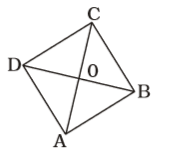
∠ABC = 60°
AB = BC

Correct Option: A

According to question , we draw a figure of rhombus ABCD in which AC is its smallest diagonal

∠ABC = 60°
AB = BC
∴ ∠BAC = ∠BCA = 60°
∴ ∆ ABC is an equilateral triangle.

As per the given in question , we draw a figure cyclic trapezium ABCD

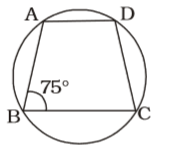
Given , ∠ABC = 75°
ABCD is a concyclic quadrilateral.
AD || BC
∴ ∠DAB + ∠ABC = 180°
⇒ ∠DAB = 180° – 75° = 105°
Sum of the opposite of a concyclic quadrilateral = 180°

Correct Option: A

As per the given in question , we draw a figure cyclic trapezium ABCD

Given , ∠ABC = 75°
ABCD is a concyclic quadrilateral.
AD || BC
∴ ∠DAB + ∠ABC = 180°
⇒ ∠DAB = 180° – 75° = 105°
Sum of the opposite of a concyclic quadrilateral = 180°
∴ ∠BAD + ∠BCD = 180°
⇒ 105° + ∠BCD = 180°
⇒ ∠BCD = 180° – 105° = 75°

On the basis of question we draw a figure of rhombus ABCD

In the rhombus PQRS,
PQ = QR = RS = SP
∠SPQ = 50°

Correct Option: B

On the basis of question we draw a figure of rhombus ABCD

In the rhombus PQRS,
PQ = QR = RS = SP
∠SPQ = 50°