Plane Geometry
-
In ∆ABC, ∠A = 90°, BP and CQ are two medians. Then the value of BP² + CQ² BC²
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,

In ∆ AQC,
∠A = 90°
⇒ CQ² = AC² + QA²
⇒ 4CQ² = 4AC² + 4QA²
⇒ 4CQ² = 4AC² + (2QA)²
⇒ 4CQ² = 4AC² + AB²
[∵AB = 2QA]
In ∆ BPA,
BP² = BA² + AP²
⇒ 4BP² = 4BA² + 4AP²
⇒ 4BP² = 4BA² + AC²
[∵ AC = 2AP]
∴ 4 CQ² + 4 BP² = 4 AC² + AB² + 4 AB² + AC²
⇒ 4(CQ² + BP²) = 5(AC² + AB²) = 5 BC²Correct Option: B
On the basis of given in question , we draw a figure triangle ABC ,

In ∆ AQC,
∠A = 90°
⇒ CQ² = AC² + QA²
⇒ 4CQ² = 4AC² + 4QA²
⇒ 4CQ² = 4AC² + (2QA)²
⇒ 4CQ² = 4AC² + AB²
[∵AB = 2QA]
In ∆ BPA,
BP² = BA² + AP²
⇒ 4BP² = 4BA² + 4AP²
⇒ 4BP² = 4BA² + AC²
[∵ AC = 2AP]
∴ 4 CQ² + 4 BP² = 4 AC² + AB² + 4 AB² + AC²
⇒ 4(CQ² + BP²) = 5(AC² + AB²) = 5 BC²⇒ BP² + CQ² = 5 BC² 4
- In ∆ ABC, AB = AC, O is a point on BC such that BO = CO and OD is perpendicular to AB and OE is perpendicular to AC. If ∠BOD = 30° then measure of ∠AOE is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
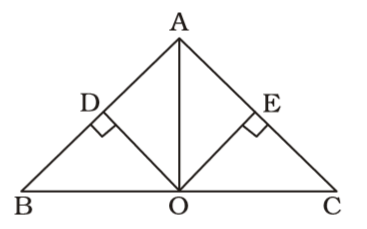
∠BDO = 90°
∠BOD = 30°
∴ ∠DBO = 60°
∠B = ∠C = 60°
∴ ∠EOC = 30°
AO is bisector of BC.Correct Option: B
As per the given in question , we draw a figure of triangle ABC

∠BDO = 90°
∠BOD = 30°
∴ ∠DBO = 60°
∠B = ∠C = 60°
∴ ∠EOC = 30°
AO is bisector of BC.
∴ ∠DOE = 120°
∴ ∠AOE = ∠AOD = 60°
- O is the orthocentre of ∆ ABC. Then ∠BOC + ∠BAC is equal to
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure in which O is the orthocentre of ∆ ABC ,

∴ ∠BOC = 180° – ∠ACorrect Option: C
Firstly , We draw a figure in which O is the orthocentre of ∆ ABC ,

∴ ∠BOC = 180° – ∠A
⇒ ∠BOC + ∠BAC = 180°
- In a triangle ABC, if ∠A + ∠C = 140° and ∠A + ∠B = 180°, then ∠A is equal to
-
View Hint View Answer Discuss in Forum
Given that , ∠A + ∠C = 140° and ∠A + ∠B = 180°
In a ∆ ABC,
We know that , ∠A + ∠B + ∠C = 180°
⇒ ∠B + 140° = 180°
⇒ ∠B = 180° – 140° = 40°
∴ ∠A + 3 ∠B = 180°Correct Option: C
Given that , ∠A + ∠C = 140° and ∠A + ∠B = 180°
In a ∆ ABC,
We know that , ∠A + ∠B + ∠C = 180°
⇒ ∠B + 140° = 180°
⇒ ∠B = 180° – 140° = 40°
∴ ∠A + 3 ∠B = 180°
⇒ ∠A + 3 × 40° = 180°
⇒ ∠A = 180° – 120° = 60°.
- In ∆ABC , ∠B = 60° , and ∠C = 40° , AD and AE are respectively the bisector of ∠A and perpendicular on BC. The measure of ∠EAD is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure triangle ABC

∠B + ∠C = 60° + 40° = 100°
∴ ∠A = 180° – 100° = 80°
∴ ∠BAD = 40°
In ∆ ABE,
∠AEB = 90°Correct Option: B
As per the given in question , we draw a figure triangle ABC

∠B + ∠C = 60° + 40° = 100°
∴ ∠A = 180° – 100° = 80°
∴ ∠BAD = 40°
In ∆ ABE,
∠AEB = 90°
∴ ∠BAE = 180° – 90° – 60° = 30°
∴ ∠EAD = ∠BAD – ∠BAE = 40° – 30° = 10°

