Plane Geometry
- The tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C intersects the other two tangents at Q and R, then the measure of the ∠QPR is
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre P whose the tangents are drawn at the extremities of diameter AB ,
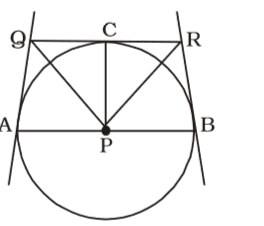
In ∆ PCR and ∆ RBP,
PC = PB (radii)
RC = RB
PR is common.
∴ ∆PCR ≌ ∆RBP [By SSS]Correct Option: C
According to question , we draw a figure of a circle with centre P whose the tangents are drawn at the extremities of diameter AB ,

In ∆ PCR and ∆ RBP,
PC = PB (radii)
RC = RB
PR is common.
∴ ∆PCR ≌ ∆RBP [By SSS]
∴ ∠CPR = ∠RPB
Similarly, ∠CPQ = ∠QPA
∴ ∠QPR = 90°
[∴ ∠APB = 180°]
- If a chord of a circle of radius 5 cm is a tangent to another circle of radius 3 cm, both the circles being concentric, then the length of the chord is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two concentric circles with centre O,
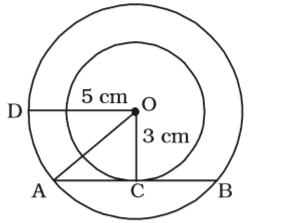
AC = √AO² - OC²
AC = √5² - 3²Correct Option: C
As per the given in question , we draw a figure of two concentric circles with centre O,

AC = √AO² - OC²
AC = √5² - 3²
AC = √25 - 9
AC = √16 = 4 cm
∴ AB = 2 × 4 = 8 cm
- A chord of length 39 cm is at a distance of 10.4 cm from the centre of a circle. Find the radius of the circle.
-
View Hint View Answer Discuss in Forum
On the basis of question we draw a figure of a circle with centre O
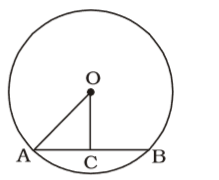
OC ⊥ AB∴ AC = CB = 39 = 19.5 cm. 2
OC = 10.4 cm
∴ Radius of circle = OA = √OC² + CA²
OA = √(10.4)² + (19.5)²
Correct Option: B
On the basis of question we draw a figure of a circle with centre O

OC ⊥ AB∴ AC = CB = 39 = 19.5 cm. 2
OC = 10.4 cm
∴ Radius of circle = OA = √OC² + CA²
OA = √(10.4)² + (19.5)²
OA = √108.16 + 380.25
OA = √488.41 = 22.1 cm
- Length of a chord PQ of a circle with centre O is 4 cm. If the distance of PQ from the point O is 2 cm, then the length of the diameter is:
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a circle with centre O ,
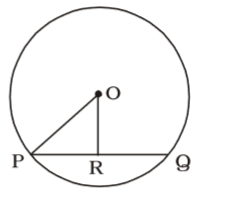
OR ⊥ PQ∴ PR = RQ = 4 = 2 cm. 2
OR = 2 cm
In ∆ OPR,
OP = √PR² + RO²
OP = √2² + 2² = √4 + 4
Correct Option: D
According to question , we draw a figure of a circle with centre O ,

OR ⊥ PQ∴ PR = RQ = 4 = 2 cm. 2
OR = 2 cm
In ∆ OPR,
OP = √PR² + RO²
OP = √2² + 2² = √4 + 4
OP = √8 = 2√2 cm
∴ Diameter = 2OP = 2 × 2√2 = 4√2 cm
- Two circles touch each other internally. The radius of the smaller circle is 6 cm and the distance between the centre of two circles is 3 cm. The radius of the larger circle is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of two circles touch each other internally ,
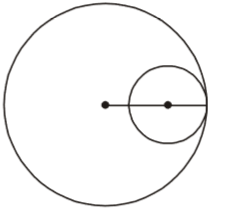
Given , The radius of the smaller circle = 6 cm
and the distance between the centre of two circles = 3 cm.Correct Option: B
As per the given in question , we draw a figure of two circles touch each other internally ,

Given , The radius of the smaller circle = 6 cm
and the distance between the centre of two circles = 3 cm.
∴ Radius of larger circle = 6 + 3 = 9 cm.

