Plane Geometry
- In ∆ ABC, D and E are two mid points of sides AB and AC respectively. If ∠BAC = 40° and ∠ABC = 65° then ∠CED is :
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC in which D and E are two mid points of sides AB and AC respectively.
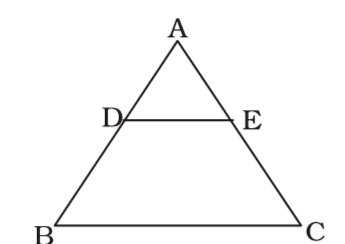
Here , ∠BAC = 40°, ∠ABC = 65°
∴ ∠ACB = 180° – ∠BAC - ∠ABC = 180° - 40° – 65° = 75°
DE || BCCorrect Option: D
Firstly , We draw a figure of triangle ABC in which D and E are two mid points of sides AB and AC respectively.

Here , ∠BAC = 40°, ∠ABC = 65°
∴ ∠ACB = 180° – ∠BAC - ∠ABC = 180° - 40° – 65° = 75°
DE || BC
∴ ∠AED = ∠ACB = 75°
∴ ∠CED = 180° – 75° = 105°
- O is the orthocentre of ∆ ABC. Then ∠BOC + ∠BAC is equal to
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure in which O is the orthocentre of ∆ ABC ,

∴ ∠BOC = 180° – ∠ACorrect Option: C
Firstly , We draw a figure in which O is the orthocentre of ∆ ABC ,

∴ ∠BOC = 180° – ∠A
⇒ ∠BOC + ∠BAC = 180°
- In ∆ ABC, AB = AC, O is a point on BC such that BO = CO and OD is perpendicular to AB and OE is perpendicular to AC. If ∠BOD = 30° then measure of ∠AOE is
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of triangle ABC
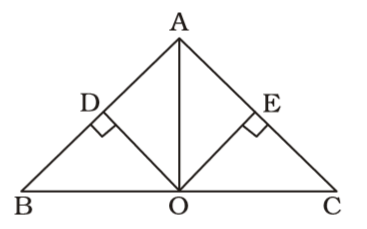
∠BDO = 90°
∠BOD = 30°
∴ ∠DBO = 60°
∠B = ∠C = 60°
∴ ∠EOC = 30°
AO is bisector of BC.Correct Option: B
As per the given in question , we draw a figure of triangle ABC

∠BDO = 90°
∠BOD = 30°
∴ ∠DBO = 60°
∠B = ∠C = 60°
∴ ∠EOC = 30°
AO is bisector of BC.
∴ ∠DOE = 120°
∴ ∠AOE = ∠AOD = 60°
-
In ∆ABC, ∠A = 90°, BP and CQ are two medians. Then the value of BP² + CQ² BC²
-
View Hint View Answer Discuss in Forum
On the basis of given in question , we draw a figure triangle ABC ,

In ∆ AQC,
∠A = 90°
⇒ CQ² = AC² + QA²
⇒ 4CQ² = 4AC² + 4QA²
⇒ 4CQ² = 4AC² + (2QA)²
⇒ 4CQ² = 4AC² + AB²
[∵AB = 2QA]
In ∆ BPA,
BP² = BA² + AP²
⇒ 4BP² = 4BA² + 4AP²
⇒ 4BP² = 4BA² + AC²
[∵ AC = 2AP]
∴ 4 CQ² + 4 BP² = 4 AC² + AB² + 4 AB² + AC²
⇒ 4(CQ² + BP²) = 5(AC² + AB²) = 5 BC²Correct Option: B
On the basis of given in question , we draw a figure triangle ABC ,

In ∆ AQC,
∠A = 90°
⇒ CQ² = AC² + QA²
⇒ 4CQ² = 4AC² + 4QA²
⇒ 4CQ² = 4AC² + (2QA)²
⇒ 4CQ² = 4AC² + AB²
[∵AB = 2QA]
In ∆ BPA,
BP² = BA² + AP²
⇒ 4BP² = 4BA² + 4AP²
⇒ 4BP² = 4BA² + AC²
[∵ AC = 2AP]
∴ 4 CQ² + 4 BP² = 4 AC² + AB² + 4 AB² + AC²
⇒ 4(CQ² + BP²) = 5(AC² + AB²) = 5 BC²⇒ BP² + CQ² = 5 BC² 4
- If the sides of a triangle are extended in both the sides then the sum of the exterior angles so formed in both sides is
-
View Hint View Answer Discuss in Forum
Firstly , We draw a figure of triangle ABC extended in both the sides ,

As we know that , ∠ABC + ∠BCA + ∠BAC = 180°
Again, ∠ACB + ∠ACD = 180°
∠ABC + ∠ABF = 180°
∠BAC + ∠EAC = 180°Correct Option: C
Firstly , We draw a figure of triangle ABC extended in both the sides ,

As we know that , ∠ABC + ∠BCA + ∠BAC = 180°
Again, ∠ACB + ∠ACD = 180°
∠ABC + ∠ABF = 180°
∠BAC + ∠EAC = 180°
∴ ∠ACD + ∠ABF + ∠CAE = 540 – 180° = 360°
∴ Required answer = 2 × 360° = 720 °

