Plane Geometry
- ABC is a right angled triangle with a right angle at A. Points D, E are the middle points of AB and AC respectively. Which of the following relations is correct ?
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a right angled triangle ABC
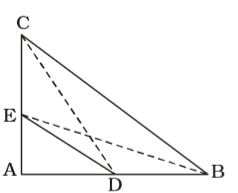
Using Pythagoras theorem.
BE² = AE² + AB²
CD² = AC² + AD²
∴ BE² + CD² = AE² + AD² + AB² + AC²BE² + CD² = 
AC 
² + 
AB 
² + AB² + AC² 2 2
Correct Option: B
According to question , we draw a figure of a right angled triangle ABC

Using Pythagoras theorem.
BE² = AE² + AB²
CD² = AC² + AD²
∴ BE² + CD² = AE² + AD² + AB² + AC²BE² + CD² = 
AC 
² + 
AB 
² + AB² + AC² 2 2 BE² + CD² = AC² + AB² + AB² + AC² 4 4
⇒ 4 (BE² + CD²) = 5 (AB² + AC²) = 5BC²
- PQRS is a rhombus in which ∠SPQ = 64°. Equilateral triangles PXQ and QYR are drawn outside the rhombus on sides PQ and QR. Calculate the magnitude of the angle ∠QXY.
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a rhombus PQRS and Equilateral triangles PXQ and QYR are drawn outside the rhombus on sides PQ and QR
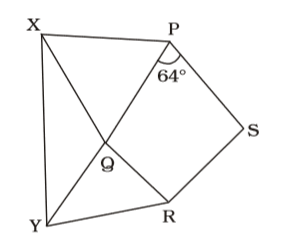
∠SPQ = 64°
∴ ∠PQR + ∠SPQ = 180°
∠PQR = 180° – 64° = 116°
As we know that each angle of equilateral triangle is 60°.
∴ ∠XQY = 360° – 116° – 60° – 60° = 124°Correct Option: B
As per the given in question , we draw a figure of a rhombus PQRS and Equilateral triangles PXQ and QYR are drawn outside the rhombus on sides PQ and QR

∠SPQ = 64°
∴ ∠PQR + ∠SPQ = 180°
∠PQR = 180° – 64° = 116°
As we know that each angle of equilateral triangle is 60°.
∴ ∠XQY = 360° – 116° – 60° – 60° = 124°∴ ∠QXY = 180° - 124° = 56° = 28° 2 2
- P, Q and R are the points so that PR = 3 cm, QR = 5 cm and PQ = 8 cm. The number of circles passing through the points P, Q and R is :
-
View Hint View Answer Discuss in Forum
According to question , we draw a figure of a line with P, Q and R points

Given that , PR = 3 cm, QR = 5 cm and PQ = 8 cmCorrect Option: D
According to question , we draw a figure of a line with P, Q and R points

Given that , PR = 3 cm, QR = 5 cm and PQ = 8 cm
PR + RQ = PQ
Hence, P, Q and R are collinear. Hence, no circle will pass through these three points.
- The three angles of a triangle are in the ratio 3 : 4 : 5. Then the angles respectively are :
-
View Hint View Answer Discuss in Forum
According to question ,
In ∆ ABC,
As we know that, ∠A + ∠B + ∠C = 180°
Sum of ratio angles = 12
Given , A : B : C = 3 : 4 : 5∴ ∠A = 3 × 180° = 45° 12
Correct Option: A
According to question ,
In ∆ ABC,
As we know that, ∠A + ∠B + ∠C = 180°
Sum of ratio angles = 12
Given , A : B : C = 3 : 4 : 5∴ ∠A = 3 × 180° = 45° 12 ∠B = 4 × 180° = 60° 12 ∠C = 5 × 180° = 75° 12
- If D, E and F are the mid points of BC, CA and AB respectively of the ∆ ABC then the ratio of area of the parallelogram DEFB and area of the trapezium CAFD is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure a ∆ ABC
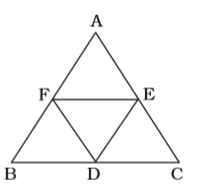
D and E are midpoints of BC and AC respectively.
∴ DE || BA ⇒ DE || BF,
FE || BD
DF is the diagonal of parallelogram BDEF.
∴ Area of ∆ BDF = Area of ∆ DEF
Similarly DE is the diagonal of parallelogram DCEF.
∴ Area of ∆ DCE = Area of ∆ DEF
∴ ∆ BDF = ∆ DCE = ∆ AFE = ∆ DEF
∴ On adding , we get
4 × ∆ DEF = ∆ ABCParallelogram BDEF = 2 × ∆ DEF = 1 × ∆ ABC 2
Quadrilateral CAFD = ∆ABC – ∆BDF
Correct Option: A
As per the given in question , we draw a figure a ∆ ABC

D and E are midpoints of BC and AC respectively.
∴ DE || BA ⇒ DE || BF,
FE || BD
DF is the diagonal of parallelogram BDEF.
∴ Area of ∆ BDF = Area of ∆ DEF
Similarly DE is the diagonal of parallelogram DCEF.
∴ Area of ∆ DCE = Area of ∆ DEF
∴ ∆ BDF = ∆ DCE = ∆ AFE = ∆ DEF
∴ On adding , we get
4 × ∆ DEF = ∆ ABCParallelogram BDEF = 2 × ∆ DEF = 1 × ∆ ABC 2
Quadrilateral CAFD = ∆ABC – ∆BDFQuadrilateral CAFD = ∆ABC – 1 × ∆ BDF 4 = 3 × ∆ ABC 4 ∴ Required ratio = 1 × ∆ ABC : 3 × ∆ ABC = 2 : 3 2 4

