If D, E and F are the mid points of BC, CA and AB respectively

Home » Aptitude » Plane Geometry » Question

If D, E and F are the mid points of BC, CA and AB respectively of the ∆ ABC then the ratio of area of the parallelogram DEFB and area of the trapezium CAFD is :

1. 2 : 3
2. 3 : 4
3. 1 : 2
4. 1 : 3

Correct Option: A

As per the given in question , we draw a figure a ∆ ABC

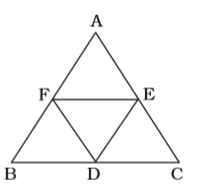
D and E are midpoints of BC and AC respectively.
∴ DE || BA ⇒ DE || BF,
FE || BD
DF is the diagonal of parallelogram BDEF.
∴ Area of ∆ BDF = Area of ∆ DEF
Similarly DE is the diagonal of parallelogram DCEF.
∴ Area of ∆ DCE = Area of ∆ DEF
∴ ∆ BDF = ∆ DCE = ∆ AFE = ∆ DEF
∴ On adding , we get
4 × ∆ DEF = ∆ ABC

Parallelogram BDEF = 2 × ∆ DEF =	1	× ∆ ABC
	2

Quadrilateral CAFD = ∆ABC – ∆BDF

Quadrilateral CAFD = ∆ABC –	1	× ∆ BDF
	4

=	3	× ∆ ABC
	4

∴ Required ratio =	1	× ∆ ABC :	3	× ∆ ABC = 2 : 3
	2		4