Plane Geometry
- If angles of measure (5y + 62°) and (22° + y) are supplementary, then value of y is :
-
View Hint View Answer Discuss in Forum
As we know that Sum of two supplementary angles = 180°
∴ ( 5y + 62° ) + ( 22° + y ) = 180°
⇒ 6y + 84° = 180°
⇒ 6y = 180° – 84° = 96°Correct Option: A
As we know that Sum of two supplementary angles = 180°
∴ ( 5y + 62° ) + ( 22° + y ) = 180°
⇒ 6y + 84° = 180°
⇒ 6y = 180° – 84° = 96°∴ y = 96 = 16° 6
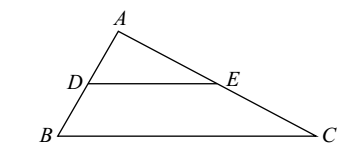
- In, ΔABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
-
View Hint View Answer Discuss in Forum
Clearly DE || BC (by converse of BPT)
∴ ΔADE ∼ ABC (∠A = ∠A and ∠ADE = ∠B)∴ Area (∆ADE) = AD2 (Area Theorem) Area (∆ABC) AB2 Correct Option: B
Clearly DE || BC (by converse of BPT) ∴ ΔADE ∼ ABC (∠A = ∠A and ∠ADE = ∠B)
∴ area (∆ADE) = AD2 (Area Theorem) area (∆ABC) AB2 = AD2 = 1 (∴AB = 2AD) (2AD)2 4
- A vertical stick 12 cm long casts a shadow 8 cm long on the ground. At the same time a tower casts the shadow 40 m long on the ground. Find the height of the tower.
-
View Hint View Answer Discuss in Forum
Draw a figure as per given question,
In ΔACB and PCQ
∠C = ∠C (common)
∠ABC = ∠PQC (each 90°)
∴ ΔACB ∼ ΔPC (AA Similarity)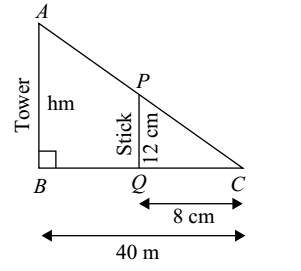
Correct Option: C
In ΔACB and PCQ
∠C = ∠C (common)
∠ABC = ∠PQC (each 90°)
∴ ΔACB ∼ ΔPC (AA Similarity)∴ AB = BC PQ QC h = 4000 12 8
h = 60m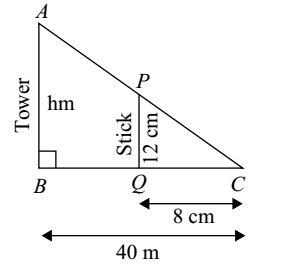
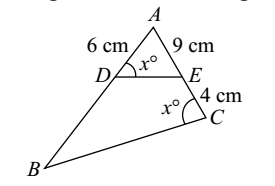
- In the given figure, find the length of BD.
-
View Hint View Answer Discuss in Forum
In Δs ADE and ΔABC
∠A = ∠A [common]
∠ADE = ∠ACB = x° (Given)
∴ ΔADE ∼ ΔACB ( AA Similarly)Correct Option: A
In ΔsADE and ΔABC
∠A = ∠A [common]
∠ADE = ∠ACB = x°(Given)
∴ ΔADE ∼ ΔACB (AA Similarly)AD = AE (corresponding side of ⁓ ∆s are proportional) AC AB 6 = 9 13 AB AB = 39 = 19.5 cm 2
Hence BD = AB - AD = 19.5 - 6 = 13.5 cm.
- ABCD is a quadrilateral inscribed in a circle with centre O. If ∠COD = 120° and ∠BAC = 30°, then ∠BCD is :
-
View Hint View Answer Discuss in Forum
As per the given in question , we draw a figure of a quadrilateral ABCD inscribed in a circle with centre O
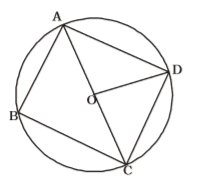
Given , ∠COD = 120°
∠BAC = 30°∠CAD = 1 × ∠COD 2 ∠CAD = 1 × 120° = 60° 2
Correct Option: B
As per the given in question , we draw a figure of a quadrilateral ABCD inscribed in a circle with centre O

Given , ∠COD = 120°
∠BAC = 30°∠CAD = 1 × ∠COD 2 ∠CAD = 1 × 120° = 60° 2
∴ ∠BAD = 90°
∴ ∠BCD = 180° - ∠BAD
∴ ∠BCD = 180° – 90° = 90°

