Firstly , We draw a figure of an isosceles triangle ABC ,

Given that , AB = AC and ∠B = 35°
⇒ ∠ABC = ∠ACB = 35°
Now, ∠ADB = 90°

Correct Option: D

Firstly , We draw a figure of an isosceles triangle ABC ,

Given that , AB = AC and ∠B = 35°
⇒ ∠ABC = ∠ACB = 35°
Now, ∠ADB = 90°
In ∆ADB , ∠ BAD + ∠ ABD + ∠ ADB = 180°
⇒ ∠ BAD + 90° + 35° = 180°
∴ ∠BAD = 55°

As per the given in question , we draw a figure of an isosceles triangle ABC ,

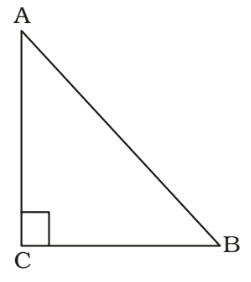
In isosceles triangle ,
AC = BC = 5 cm
∴ AB = √AB² + BC²
AB = √5² + 5²

Correct Option: C

As per the given in question , we draw a figure of an isosceles triangle ABC ,

In isosceles triangle ,
AC = BC = 5 cm
∴ AB = √AB² + BC²
AB = √5² + 5²
AB = √50 = 5√2cm

if three altitudes are equal, then the triangle is called equilateral.

Correct Option: B

We know that in a triangle, if three altitudes are equal, then the triangle is called equilateral.

Since DE || BC, We can use the formula,

Correct Option: A

Since DE || BC,

complement of 30°20′ = 90° – ( 30°20′ ) = 90° – ( 30° + 20′ )
= (89° – 30°) + (1° – 20′)

Correct Option: B

complement of 30°20′ = 90° – ( 30°20′ ) = 90° – ( 30° + 20′ )
= (89° – 30°) + (1° – 20′)
= 59° + 60′ – 20′ [ ∴ 1° = 60°′]
= 59° + 40′ = 59°40′.