Plane Geometry
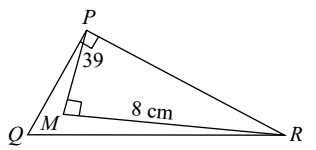
- In the given figure ∠QPR = 90°, QR = 26 cm, PM = 6 cm, MR = 8 cm and ∠PMR = 90°, find the area of ΔPQR.
-
View Hint View Answer Discuss in Forum
Given in the question, QR = 26 cm, PM = 6 cm, MR = 8 cm
According to question, in Δ PMR
PR = √PM2 + MR2 (Pythagoras Theorem)
According to question, in Δ PQR
PQ = √QR2 - PR2 (Pythagoras Theorem)Correct Option: C
Given in the question, QR = 26 cm, PM = 6 cm, MR = 8 cm
According to question, in Δ PMR
(Pythagoras Theorem)
PR = √PM2 + MR2 = √36 + 64 = √ 100 = 10 cm
According to question, in Δ PQR
(Pythagoras Theorem)
PQ = √QR2 - PR2 = √262 - 102 = √576 - 100 = √ 476 = 24
∴ area of triangle ∆PQR = Base length x Height / 2
⇒ area of triangle ∆PQR = PR x PQ / 2
⇒ area of triangle ∆PQR = 10 x 24 / 2 = 10 x 12
⇒ area of triangle ∆PQR = 120
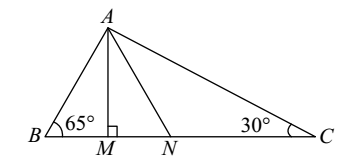
- In the given figure, AM ⊥ BC and AN is the bisector of ∠A. What is the measure of ∠MAN.
-
View Hint View Answer Discuss in Forum
Use the formula,
∠MAN = 1 (∠B - ∠C) 2 Correct Option: A
Use the formula,
∠MAN = 1 (∠B - ∠C) 2 ∠MAN = 1 (65° - 30°) 2 ∠MAN = 1 (35°) 2
∠MAN = 17.5°
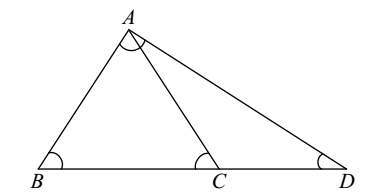
- In the given figure, ∠B = ∠C = 55° and ∠D = 25°. Then:
-
View Hint View Answer Discuss in Forum
According to question,
∠B = ∠C = 55° , ∠D = 25°
We can say ,
AB = AC ( ∴ ∠B = ∠C = 55° )
In Triangle ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 55° + 55° = 180°
⇒ ∠A + 110° = 180°
⇒ ∠A = 180° - 110°
⇒ ∠A = 70° ..........................(1)
As per given figure,
∠ACD + ∠ACB = 180° ( ∠ACB = ∠C = 55°)
⇒ ∠ACD + 55° = 180°
⇒ ∠ACD = 180° - 55°
⇒ ∠ACD = 125° ....................... (2)
Now in Triangle ACD,
∠CAD + ∠ACD + ∠CDA = 180°
⇒ ∠CAD + 125° + 25° = 180°
⇒ ∠CAD + 150° = 180°
⇒ ∠CAD = 30° ...........................(3)Correct Option: D
According to question,
∠B = ∠C = 55° , ∠D = 25°
We can say ,
AB = AC ( ∴ ∠B = ∠C = 55° )
In Triangle ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 55° + 55° = 180°
⇒ ∠A + 110° = 180°
⇒ ∠A = 180° - 110°
⇒ ∠A = 70° ..........................(1)
As per given figure,
∠ACD + ∠ACB = 180° ( ∠ACB = ∠C = 55°)
⇒ ∠ACD + 55° = 180°
⇒ ∠ACD = 180° - 55°
⇒ ∠ACD = 125° ....................... (2)
Now in Triangle ACD,
∠CAD + ∠ACD + ∠CDA = 180°
⇒ ∠CAD + 125° + 25° = 180°
⇒ ∠CAD + 150° = 180°
⇒ ∠CAD = 30° ...........................(3)
( In a Δ, greater angle has longer side opposite to it )
From the equation (1) , (2) and (3);
∠B < ∠A and ∠CAD > ∠D ;
∴ BC > CA and CA < CD
- If two parallel lines are intersected by a transversal, then the bisectors of the two pairs of interior angles enclose a:
-
View Hint View Answer Discuss in Forum
∠AGH = ∠DHG (alt. int. angles)
⇒ 1 ∠AGH = 1 ∠DHG = 180 2 2
Thus, lines GM and HL are intersected by a transversal GH at G and H respectively such that pair of alternate angles are equal, i.e.,
∴ ∠HGM = ∠GHL
∴ GM || HL
Similarly, GL || HM
So, GMHL is a ||gm.
Since AB || CD and EF is a transversal
∴ ∠BGH + ∠DHG = 180° [co-interior angles]∴ 1 ∠BGH + 1 ∠DHG = 90° 2 2
But ∠LGH + ∠LHG + ∠GLH = 180°
∴ 90° + ∠GLH = 180° ⇒ ∠GLH = 90°
Thus, in ||gm GMHL, we have ∠GLH = 90°
Hence, GMHL is a rectangle.
Correct Option: B
∠AGH = ∠DHG (alt. int. angles)
⇒ 1 ∠AGH = 1 ∠DHG = 180 2 2
Thus, lines GM and HL are intersected by a transversal GH at G and H respectively such that pair of alternate angles are equal, i.e.,
∴ ∠HGM = ∠GHL
∴ GM || HL
Similarly, GL || HM
So, GMHL is a ||gm.
Since AB || CD and EF is a transversal
∴ ∠BGH + ∠DHG = 180° [co-interior angles]∴ 1 ∠BGH + 1 ∠DHG = 90° 2 2
But ∠LGH + ∠LHG + ∠GLH = 180°
∴ 90° + ∠GLH = 180° ⇒ ∠GLH = 90°
Thus, in ||gm GMHL, we have ∠GLH = 90°
Hence, GMHL is a rectangle.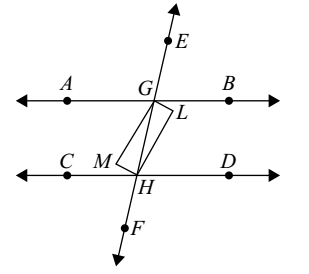
- In the given figure, OP bisect ∠BOC and OQ bisects ∠AOC. Then ∠POQ is equal to :

-
View Hint View Answer Discuss in Forum
Since OP bisects ∠BOC,
∴ ∠BOC = 2∠POC
Again, OQ bisects ∠AOC,
∴ ∠AOC = 2∠QOCCorrect Option: A
Since OP bisects ∠BOC,
∴ ∠BOC = 2∠POC
Again, OQ bisects ∠AOC,
∴ ∠AOC = 2∠QOC
Since ray OC stands on line AB, ∴,
∠AOC + ∠BOC = 180°
⇒ 2∠QOC + 2∠POC = 180°
⇒ 2∠QOC + ∠POC = 180°
⇒ ∠QOC + ∠POC = 90°
⇒ ∠POQ = 90°.
The above sum can also be restated as follows; The angle between the bisectors of a linear pair of angles is a right angle.

