-
In the given figure, OP bisect ∠BOC and OQ bisects ∠AOC. Then ∠POQ is equal to :
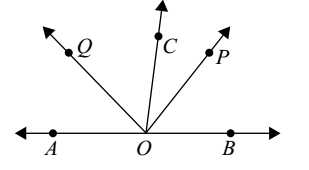
-
- 90°
- 120°
- 60°
- 100°
- None of these
Correct Option: A
Since OP bisects ∠BOC,
∴ ∠BOC = 2∠POC
Again, OQ bisects ∠AOC,
∴ ∠AOC = 2∠QOC
Since ray OC stands on line AB, ∴,
∠AOC + ∠BOC = 180°
⇒ 2∠QOC + 2∠POC = 180°
⇒ 2∠QOC + ∠POC = 180°
⇒ ∠QOC + ∠POC = 90°
⇒ ∠POQ = 90°.
The above sum can also be restated as follows; The angle between the bisectors of a linear pair of angles is a right angle.

