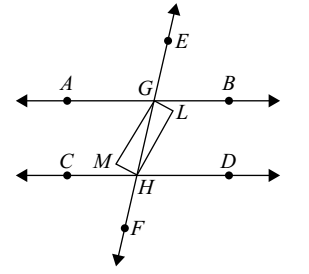
-
If two parallel lines are intersected by a transversal, then the bisectors of the two pairs of interior angles enclose a:
-
- Trapezium
- Rectangle
- Square
- circle
- None of these
Correct Option: B
∠AGH = ∠DHG (alt. int. angles)
| ⇒ | 1 | ∠AGH | = | 1 | ∠DHG | = 180 |
| 2 | 2 |
Thus, lines GM and HL are intersected by a transversal GH at G and H respectively such that pair of alternate angles are equal, i.e.,
∴ ∠HGM = ∠GHL
∴ GM || HL
Similarly, GL || HM
So, GMHL is a ||gm.
Since AB || CD and EF is a transversal
∴ ∠BGH + ∠DHG = 180° [co-interior angles]
| ∴ | 1 | ∠BGH | + | 1 | ∠DHG | = 90° |
| 2 | 2 |
But ∠LGH + ∠LHG + ∠GLH = 180°
∴ 90° + ∠GLH = 180° ⇒ ∠GLH = 90°
Thus, in ||gm GMHL, we have ∠GLH = 90°
Hence, GMHL is a rectangle.