-
In the given figure, ∠B = ∠C = 55° and ∠D = 25°. Then:
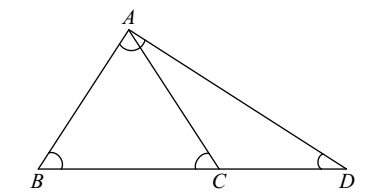
-
- BC < CA < CD
- BC > CA > CD
- BC < CA, CA > CD
- BC > CA, CA < CD
- None of these
Correct Option: D
According to question,
∠B = ∠C = 55° , ∠D = 25°
We can say ,
AB = AC ( ∴ ∠B = ∠C = 55° )
In Triangle ABC,
∠A + ∠B + ∠C = 180°
⇒ ∠A + 55° + 55° = 180°
⇒ ∠A + 110° = 180°
⇒ ∠A = 180° - 110°
⇒ ∠A = 70° ..........................(1)
As per given figure,
∠ACD + ∠ACB = 180° ( ∠ACB = ∠C = 55°)
⇒ ∠ACD + 55° = 180°
⇒ ∠ACD = 180° - 55°
⇒ ∠ACD = 125° ....................... (2)
Now in Triangle ACD,
∠CAD + ∠ACD + ∠CDA = 180°
⇒ ∠CAD + 125° + 25° = 180°
⇒ ∠CAD + 150° = 180°
⇒ ∠CAD = 30° ...........................(3)
( In a Δ, greater angle has longer side opposite to it )
From the equation (1) , (2) and (3);
∠B < ∠A and ∠CAD > ∠D ;
∴ BC > CA and CA < CD

