Plane Geometry
Geometry is a branch of Mathematics in which we study point, line, angle and different type of shapes.
Plane
It is a flat surface which has only length and breadth .
For example- surface of a table, surface of a white board etc.
Point

A point is a sharp dot.
It has no length breadth and height.
It can't be measured.
It is used to locate any thing, then it is called locator.
A point is named by a capital letter like .A
Line
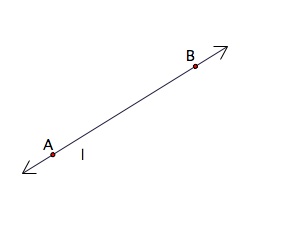
A line is a collection of points. It's starting point and ending point is endless.
Arrows on both sides of a line indicate that the line is extended both sides infinitely. It has only length but not have any width or height.
A line is named by two points on it or by a single small letter.
Line Segment

Line segments is a part of line.
It's starting and ending points are defined.
It's length is definite.
Line segment named by two capital letter like AB.
Ray
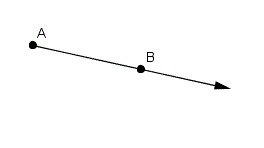
Ray is a part of line, It's one point is defined ( fixed ) and other point is endless.
Arrow of a ray indicates that ray is extended infinitely towards arrow direction.
Intersecting Lines
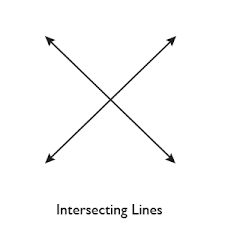
When two lines intersect each other at a point, then they are called intersecting lines.
Point through these two lines pass that point is called point of intersection.
Perpendicular Lines
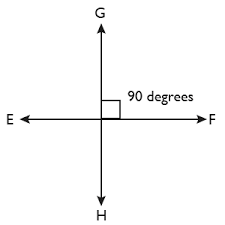
When two lines intersect each other at right angles is called perpendicular lines.
Symbol for perpendicular lines is ⊥
Concurrent Lines
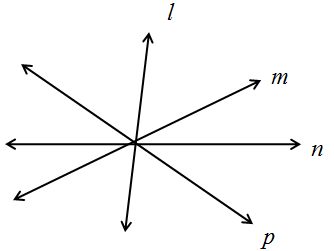
When two or more then two lines passes through a point is called concurrent lines.
Point through which these all lines pass is called point of concurrent.
Parallel Lines

When two lines lie in the same plane and never intersect each other at any point if they produced.
Perpendicular distance between them is equal.
Symbol for parallel lines is ∥.
Angle
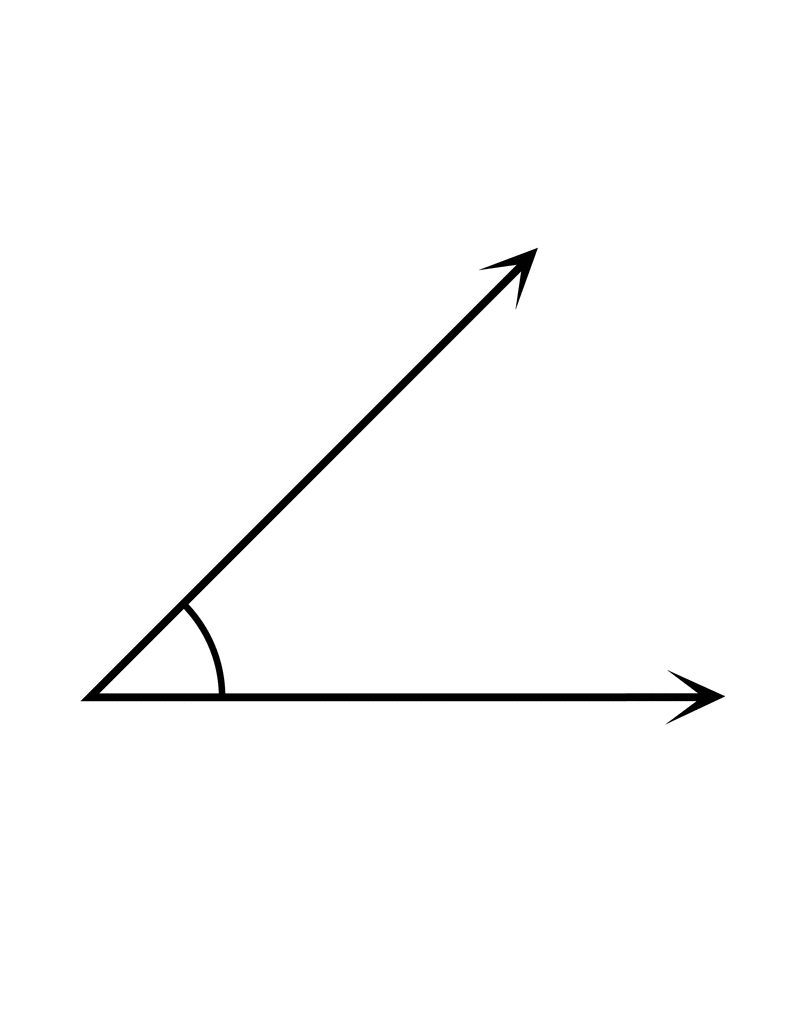
When two rays start from a common point then angle is formed.
Angle is measured in degree.
Types of Angle
Acute angle

An angle whose measure degree more than 0° but less than 90° is called acute angle. ( 0° < θ < 90° )
Obtuse angle
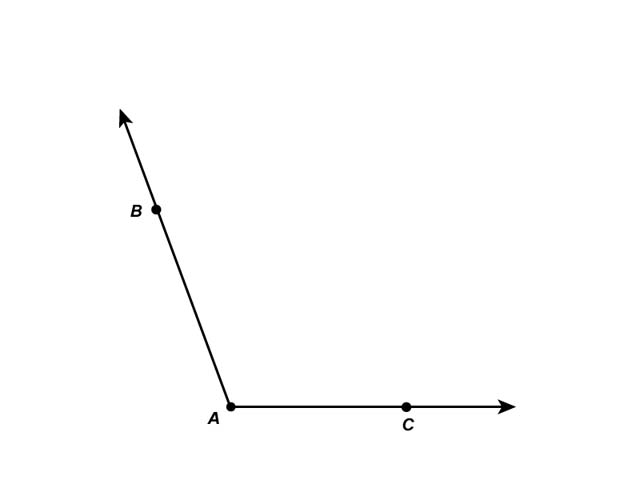
An angle whose measure degree is more than 90° but less than 180° is called obtuse angle. ( 90° < θ < 180° )
Right angle

An angle whose measure degree is equal to 90° is called right angle. ( θ = 90° )
Straight angle
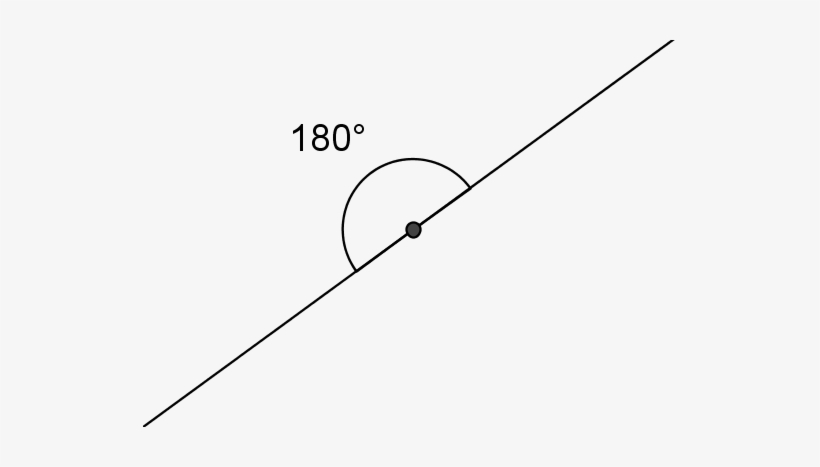
An angle whose measure degree is equal to 180° is called straight angle. ( θ = 180° )
Reflex angle
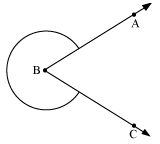
An angle whose measure degree is more than 180° but less than 360; is called reflex angle. ( 180° < θ < 360° )
Whole angle
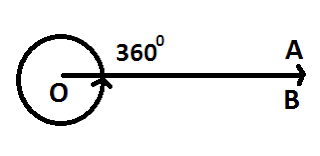
An angle whose measure degree is equal to 360° is called whole angle. ( θ = 360° )
Complementary angle
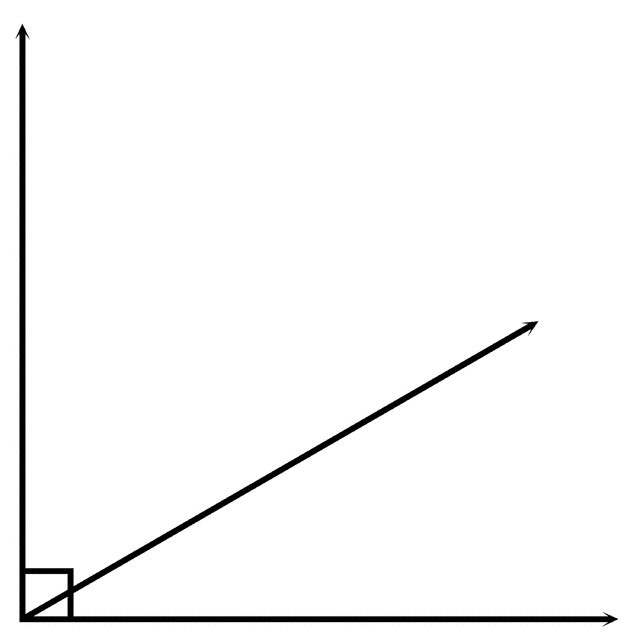
Sum of two angles is equal to 90° is called complementary angle.
Supplementary angle
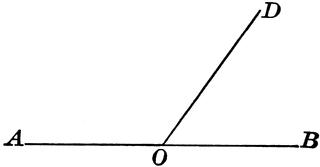
Sum of two angle is equal to 180° is called supplementary angle.
∠ AOD + ∠BOD = 180°
Vertically opposite angles
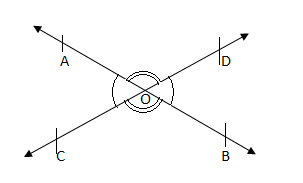
When two lines intersect then pair of opposite angles is equal and they are called pair of vertically opposite angle.
∠AOC = ∠BOD and ∠AOD = ∠BOC
Angle bisector
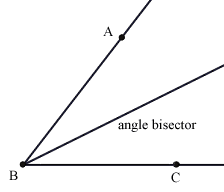
When an angle is equally divided by a line is called angle bisector.
Polygon
A closed figure which is made by three or more than three ling segments is called polygon.
Example- triangle, square, pentagon etc.
Types of Polygon
Convex polygon
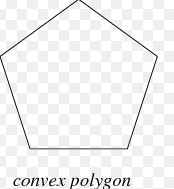
A polygon whose each interior angle is less than 180° is called convex polygon.
Concave polygon
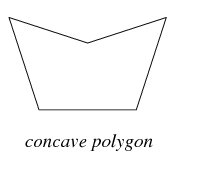
A polygon whose one interior angle is more than 180° is called concave polygon.
Regular Polygon
A polygon in which all sides and angles are equal is called regular polygon.
Irregular Polygon
A polygon in which all sides and angles are not equal is called irregular polygon.
Properties of polygons
Ex- Find the sum of all interior angles of a pentagon.
Solution:- Here, n = 5
Sum of all interior angles of a pentagon = ( n - 2 )180°
= ( 5 - 2 )180°
= 3 × 180°
= 540°
| 2. Each interior angle of a regular polygon = | × 180° | ||
| n |
Ex- Find the each interior angle of a regular hexagon.
Solution:- Here, n = 6
| Each interior angle of a regular hexagon = | × 180° | |
| n |
| = | × 180° = | × 180° | ||
| 6 | 6 |
| 4. Each exterior angle of a regular polygon = | |||
| n |
Ex- Find the each exterior angle of a regular pentagon.
Solution- Here, n = 5
| Each exterior angle of a regular pentagon = | = 72° | ||
| 5 |
| 5. Number of diagonals in a polygon = | |||
| 2 |
Ex- Find the number of diagonals in a hexagon.
Solution- Here, n = 6
| Number of diagonals in a polygon = | = | |||
| 2 | 2 |
| Number of diagonals in a polygon = | = 9 | |
| 2 |
Triangle
Triangle is a type of polygon which is made by three line segments.
It have three vertices.
Types of triangle
Triangles can be classified on the basis of their sides or angles.
On the basis of sides
Equilateral triangle
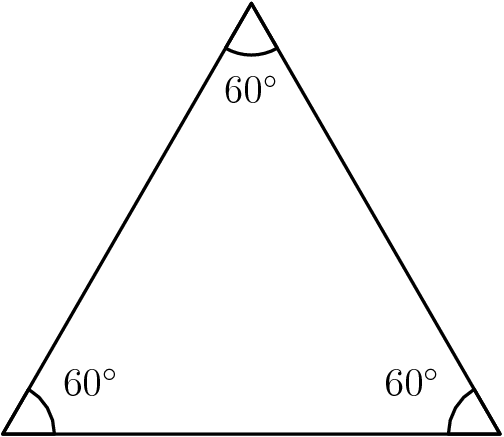
A triangle in which all three sides are equal and each angle is 60° is called an equilateral triangle.
Isosceles triangle

A triangle in which two sides are equal is called isosceles triangle.
Angle opposite to equal sides are equal.
Scalene triangle
A triangle in which all three sides are unequal is called scalene triangle
On the basis of angles
Acute angle triangle
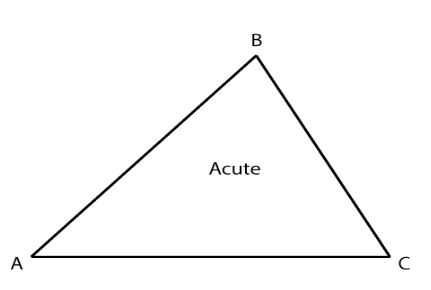
A triangle in which each angle is acute ( less than 90° ) is called an acute angle triangle.
Obtuse angle triangle

A triangle in which one angle is obtuse ( more than 90° but less than 180° ) is called obtuse angle triangle.
Right angle triangle
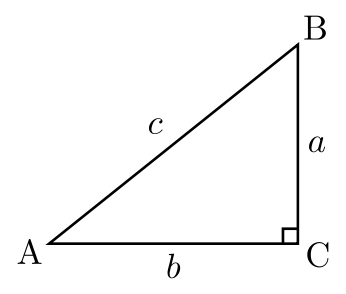
A triangle in which one angle is 90° is called right angle triangle.
Properties of Triangles
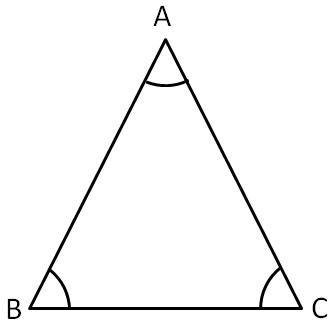
- In a triangle sum of all interior angles is 180°.
It is known as angle sum property.
In triangle ABC, ∠A + ∠B + ∠C = 180°
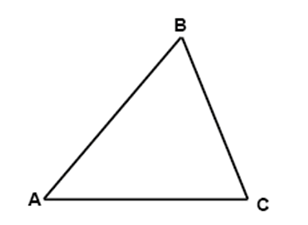
2. In a triangle sum of two sides is greater than the third side.
In triangle ABC, AB + BC > AC, BC + CA > AB, AB + AC = BC
3. In a triangle the exterior angle is equal to the sum of two opposite interior angles. ( It is known as exterior angle theorem )
∠ACD = ∠ABC + ∠BAC

4. In a triangle difference between two sides is smaller than the third side.
In triangle ABC, AB - BC < CA, BC - CA < AB, CA - AB < BC

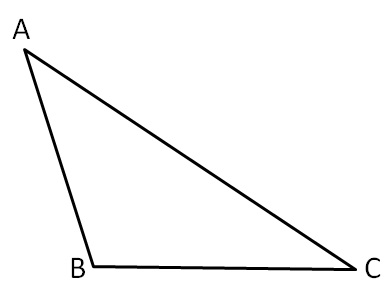
5. In a triangle side opposite to greater angle is larger side.
In triangle ABC, if ∠B > ∠C, then AC > AB
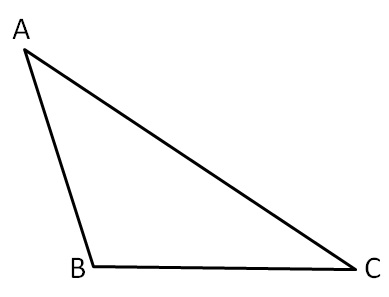
6. In a triangle side opposite to smaller angle is smaller side.
In triangle ABC, if ∠A < ∠C, then BC < AB
7. In a triangle sides opposite to equal angles are equal.
For example- In a triangle ABC, if AB = AC then ∠B = ∠C
Congruency of Two Triangles
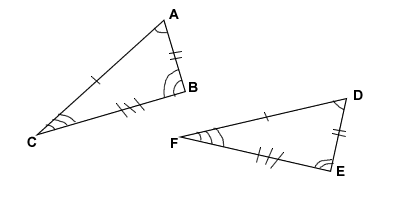
Two triangles are congruent if both triangle same shape and same size.
If two triangle are congruent, then the all three sides and all three angles of one triangle are equal to the corresponding to other triangle.
For example- If ∆ABC ≅ ∆DEF, then
AB= DE, BC= EF, AC= DF
and ∠D = ∠A, ∠E = ∠B, ∠F = ∠C
Conditions of Congruency
SAS Congruency ( Side-Angle-Side ):- When two sides and one included angle between these two side of one triangle are equal to corresponding two sides and included angle between these two sides of another triangle, then triangles are congruent.
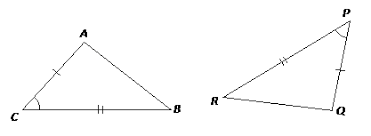
In ∆ABC and ∆PQR,
AB = PQ, ∠ACB = ∠QPR and BC = RP then
∆ABC ≅ ∆QRP,
SSS Congruency ( Side-Side-Side ):- When all three sides of one triangle are equal to corresponding all three sides of another triangle, then triangles are congruent.
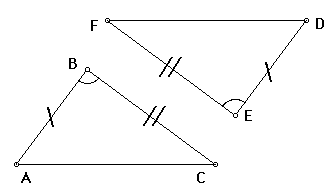
In ∆ABC and ∆DEF
AB = DE, AC = DF and BC = EF then
∆ABC ≅ ∆DEF
ASA Congruency ( Angle-Side-Angle ):- When two angles and one included side between these two angles are equal to the corresponding angles and one included side of another triangle, then triangles are congruent.
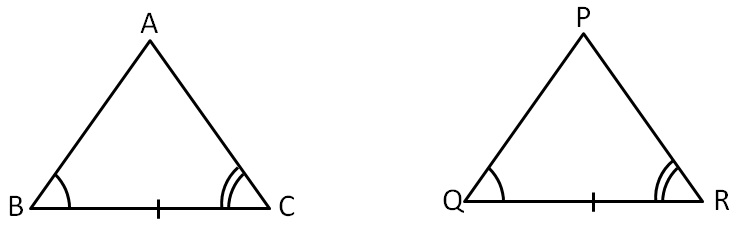
In ∆ABC and ∆PQR
∠ABC = ∠PQR, BC = QR and ∠ACB = ∠PRQ then
∆ABC ≅ ∆PQR,
RHS Congruency ( Right angle-Hypotenuse-side ):- When hypotenuse and one side of right angled triangle are equal to hypotenuse and corresponding side of another triangle.
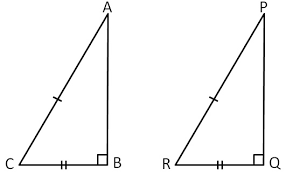
In ∆ABC and ∆PQR,
AC = PR, ∠ABC = ∠PQR = 90° and BC = QR, then
∆ABC ≅ ∆PQR
Similarity of Two Triangles
When shapes of two triangles are same but their size may or may not be equal. If two triangles are similar, then all the corresponding angles are equal and all the corresponding sides are in the same ratio.

If triangle ABC is similar to triangle DEF, then ∠P = ∠X, ∠Q = ∠ Y, ∠R = ∠Z and
| = | = | = | ||||||
| XY | YZ | XZ | Area ( ∆ DEF ) |
Condition of Similarity
AAA Similarity ( Angle-Angle-Angle ):- When all three corresponding angles are equal to another triangle, then the triangles are similar.

In ∆ABC and ∆DEF
If, ∠A = ∠D, ∠B = ∠E and ∠C = ∠F, then
∆ABC similar ∆DEF
AA Similarity ( Angle-Angle ):- When two angles of one triangle are equal to another triangle, then the triangles are similar.

In ∆ABC and ∆XYZ
If, ∠A = ∠X and ∠C = ∠Z then,
∆ABC similar ∆XYZ
SSS Similarity ( Side-Side-Side ):- When three sides of one triangle are proportional to the corresponding three sides of another triangle, then the triangles are similar.
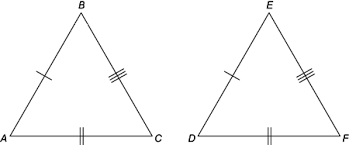
| If, | = | = | then, ∆ABC similar ∆DEF. | ||||
| DE | EF | DF |
SAS Similarity ( Side-Angle-Side ):- When two sides of a triangle are proportional to the two sides of the other triangle and the angles included between these sides of two triangles are equal.
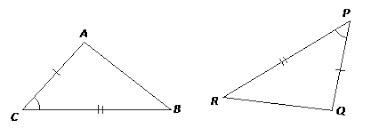
| If, | = | and ∠C = ∠P, then ∆ABC similar ∆QRP. | |||
| QP | RP |
Quadrilateral
Quadrilateral is a type of polygon in which four sides, four vertices and four angles.
Types of Quadrilateral
Parallelogram
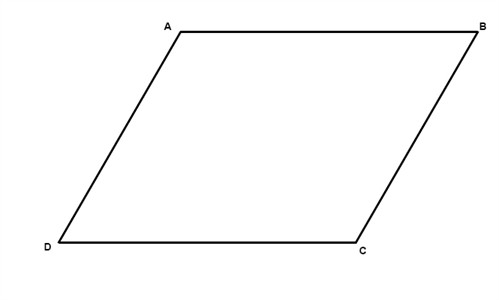
A parallelogram is a type of quadrilateral in which opposite sides are parallel and equal is called a parallelogram.
Opposite sides are equal.
Opposite sides are parallel.
Opposite angles are equal. Diagonals bisect each other.
Adjacent angles form supplementary.
Rectangle
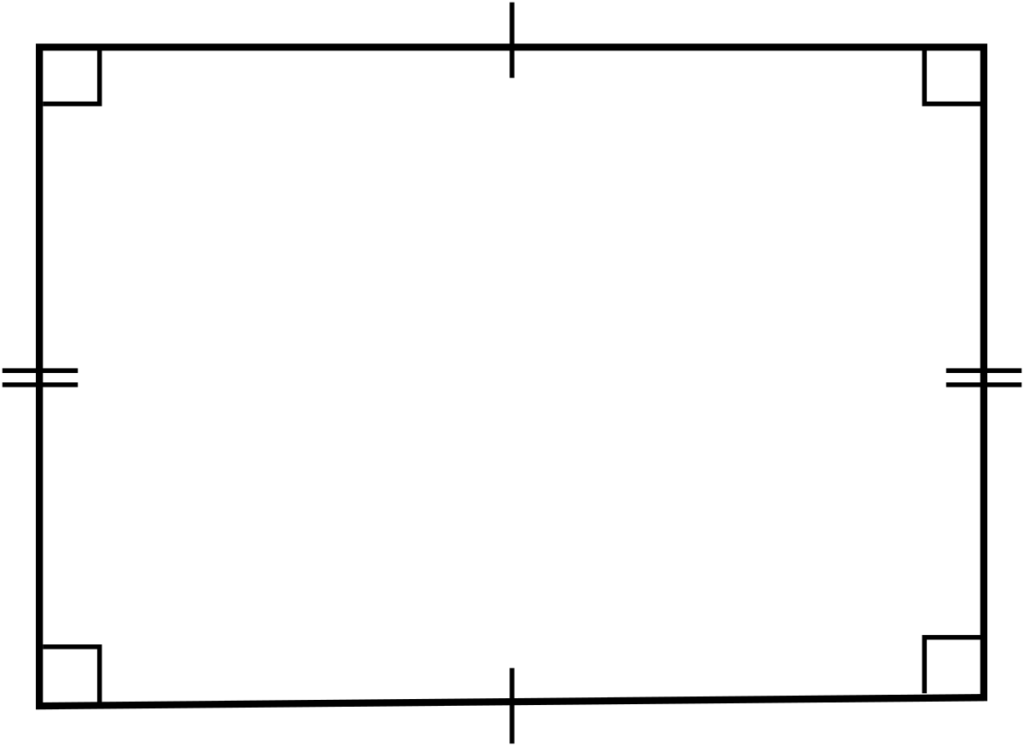
A parallelogram in which opposite sides are equal and all angles equal to 90°.
Opposite sides are equal.
Length of diagonals are equal.
Diagonals bisect each other.
Adjacent angles form supplementary.
All rectangles are parallelogram but all parallelograms are not rectangles.
Rhombus
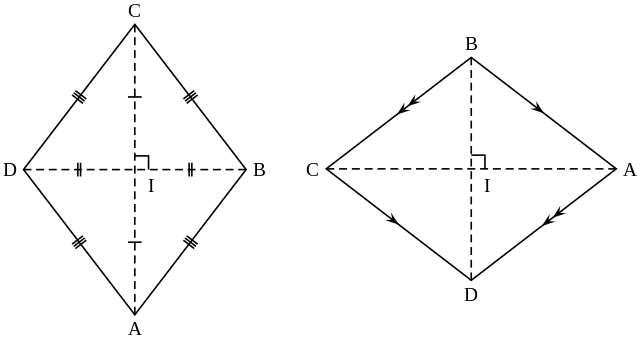
A parallelogram in which all sides are equal and diagonals bisect each other at right angle.
Opposite angles are equal.
Length of diagonals are different.
Diagonals bisect each other at 90°.
All rhombus are parallelograms but all parallelograms are not rhombus.
Square
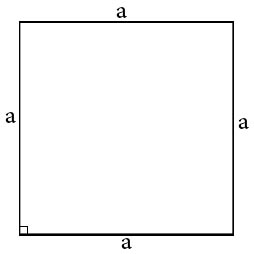
A parallelogram in which all sides are equal and each angle equal to 90°. All sides are equal.
All angles are equal to 90°.
Diagonals are equal.
Diagonals are bisect each other at 90°.
All square are rhombus but rhombus may or may not be a square.
Trapezium

A quadrilateral in which one pair of opposite sides are parallel is called trapezium.
Isosceles Trapezium
A trapezium in which non parallel sides are equal is called isosceles trapezium.
Circle
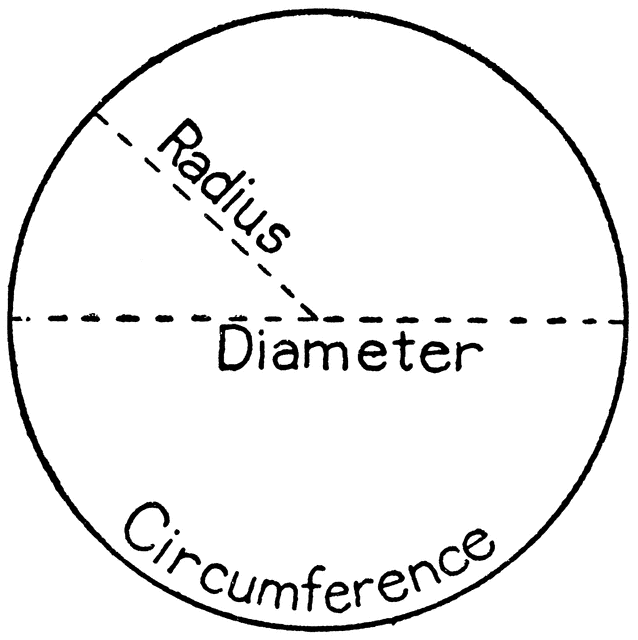
A Circle is a path of a point in a plane which moves in such a way that its distance from a fixed point always remains same. Where fixed point is called center of the circle.
Diameter
A line segments passing through the center and joins the two points on the circle is called diameter.
Diameter divides the circle into two half.
Diameter is the twice of radius. D = 2r
Circumference
Length of the boundary of a circle is called its circumference.
Chord
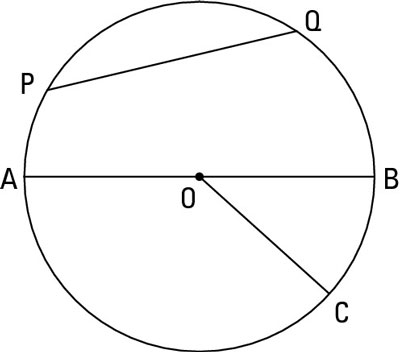
A line segment whose starting point and ending point on the circle is called a chord.
Diameter is the longest chord of the circle.
Arcs
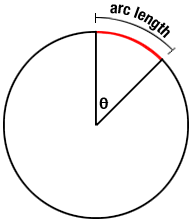
A part of the circumference of the circle between two points is called an arc.
Longer part of the circumference of the circle is called major arc and smaller part is called minor arc.
Segment
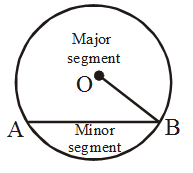
The region between a chord and an arc of a circle is called a segment. There are two segment.
The region between a chord and major arc is called a major segment.
The region between a chord and minor arc is called a minor segment.
Sector
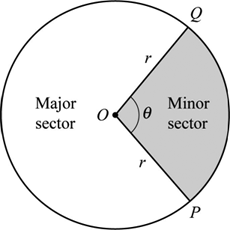
The region between an arc and two radii of a circle is called sector. There are two sectors minor and major sectors.
The region between minor arc and two radii of a circle is called minor sector.
The region between major arc and two radii of a circle is called major sector.
Tangent
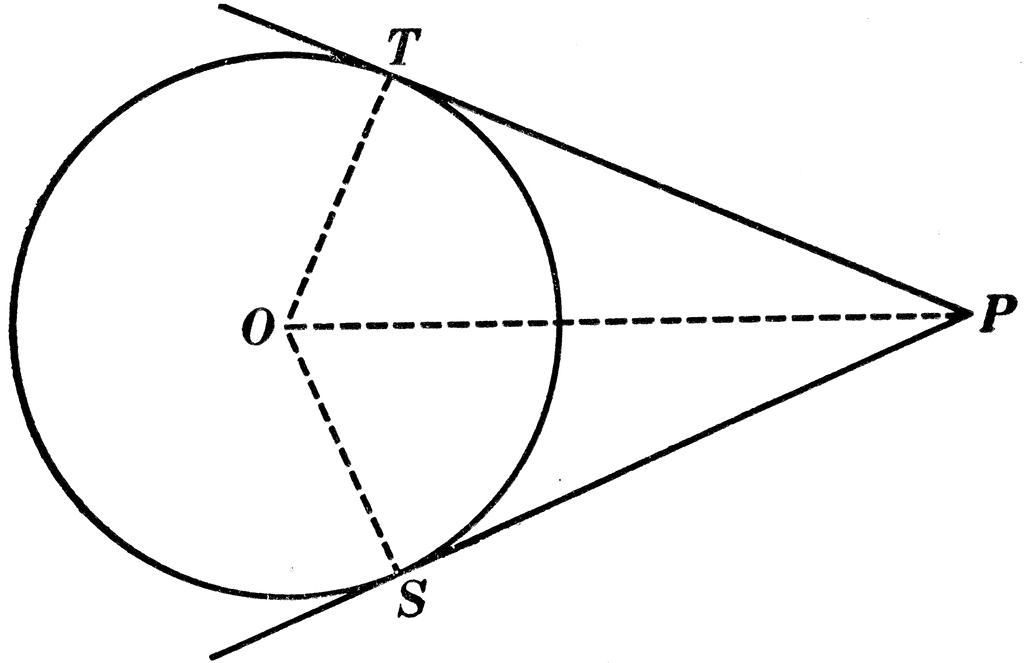
A straight line which touches the circumference of a circle at only one point is called tangent.
Properties of Tangents
- The tangent does not intersect the circumference.
- The tangent line does not cross the circle.
- Radius is always perpendicular to tangent.
- The length of two tangents drawn from the external point to the circle are equal.
Basic Properties of a Circle
- Equal chord of a circle subtend equal angles at the center.
- The perpendicular from the center of a circle to a chord of the circle bisects the chord.
- Equal chords of a circle are equidistant from the center of the circle.
- Two equal chords have equal corresponding arcs.
- The greater of the two chords is nearer to the center.
- The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
- Angle subtended by diameter on the circle is a right angle.
- Angles subtended by the same segment of a circle are equal.
- If two circles touch externally, then the distance between their centers is equal to the sum of their radii.
- If two circles touch internally the distance between their center is equal to the difference between their radii.
Cyclic Quadrilateral
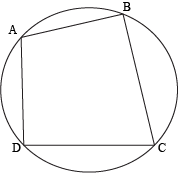
A quadrilateral in circle whose vertices on the circle is called cyclic quadrilateral.
Sum of opposite angles of a cyclic quadrilateral is 180°.