LCM and HCF
Multiples
Multiples are those numbers which are exactly divisible by a given number. Multiple of a number is always equal to or more than the given number.
For example- Multiples of 3 are (3, 6, 9, 12, …… ).
Multiples of 7 = 7, 14, 21, 28,………..
Multiples of 12 = 12, 24, 36, 48, 60, ……..
Example- Find the first five multiples of 12.
Solution:- First five multiples of 12 = 12, 24, 36, 48, 60
Common Multiple :-
A number which is exactly divisible by two or more given numbers is called common multiple.
For example- 18 is the common multiple of 2, 3, 6 and 9.
Example- Find the common multiples of 3 and 4.
Solution:- Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36,……
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44……
∴ Common multiples of 3 and 4 = 12, 24, 36,…….
LCM ( Least Common Multiple ) :-
A number which is the smallest common multiple of two or more numbers is called LCM (Least Common Multiple).
For example- Multiples of 3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, ……..
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, ……….
Common multiples of 3 and 4 = 12, 24, ……
∴ LCM of 3 and 4 = 12
Methods to find LCM :-
By Prime Factorization Method :-
To find LCM by prime factorization method, first of all, find the factors of each number. Then find the product of all the prime factors with the highest powers that occur in the given numbers.
Ex- Find the LCM of 8 and 18.
Solution:- Factors of 8 = 2 × 2 × 2 = 23
Factors of 18 = 2 × 3 × 3 = 21 × 32
LCM = 23 × 32
= 2 × 2 × 2 × 3 × 3
= 72
By Division Method :-
To find LCM by division method, first write the given numbers in a row separating them by commas. Then divide them by the smallest prime number which exactly divides the given number. Now, write down the quotients and the undivided numbers in next row. Repeat the process until all co-prime numbers are left in the last row. Then multiply all the divisors and the numbers in the last row to calculate the required LCM.
Ex- Find the LCM of 15 and 24.
Solution:- LCM = 2 × 2 × 2 × 3 × 5 = 120
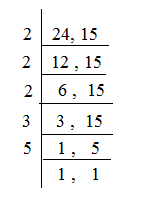
Factors :-
Numbers which exactly divide the given number are called factors.
Factors of a number are always equal to or less than the given number.
For example- Factors of 12 = 1, 2, 3, 4, 6, 12
Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24
Note- 1 is the factors of every numbers.
Example- Find all the factors of 36.
Solution:- All the factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 and 36
Methods to find all factors :-
By multiplication Method :-
In this, method, take two numbers whose product is equal to the given number.
For example- 18 = 1 × 18
18 = 2 × 9
18 = 3 × 6
18 = 6 × 3 ( Repeat )
∴ All factors of 18 = 1, 2, 3, 6, 9 and 18
Example- Find the all factors of 72.
Solution:- 72 = 1 × 72
72 = 2 × 36
72 = 3 × 24
72 = 4 × 18
72 = 6 × 12
72 = 8 × 9
72 = 9 × 8 (Repeat)
∴ All factors of 72 = 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72.
By Division Method :-
In this method divide by any number which exactly divides the given number.
For example-
48 ÷ 1 = 48
48 ÷ 2 = 24
48 ÷ 3 = 16
48 ÷ 4 = 12
48 ÷ 5 not divisible
48 ÷ 6 = 8
48 ÷ 7 not divisible
48 ÷ 8 = 6 ( Repeat )
∴ All factors of 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24 and 48
Example- Find all factors of 36.
Solution:- 36 ÷ 1 = 36
36 ÷ 2 = 18
36 ÷ 3 = 12
36 ÷ 4 = 9
36 ÷ 6 = 6
36 ÷ 9 = 4 ( Repeat )
∴ All factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18 and 36
Common Factors :-
Numbers which exactly divide each of the given numbers is called common factors. For example- 3 is the common factor of 12 and 15.
Example– Find the common factors of 18 and 24.
Solution:- Factors of 18 = 1, 2, 3, 6, 9 and 18
Factors of 24 = 1, 2, 3, 4, 6, 8, 12 and 24
∴ Common factors of 18 and 24 = 1, 2, 3 and 6
HCF ( Highest Common Factor )
A number which is the highest common factor of two or more given numbers is called highest common factor ( HCF ).
For example-
Factors of 18 = 1, 2, 3, 6, 9 and 18
Factors of 27 = 1, 3, 9 and 27
Common factors = 1, 3 and 9
Since 9 is the highest common factor of 18 and 27, then 9 is the HCF of 18 and 27.
Methods to find HCF :-
By Prime Factorization Method :-
To find the HCF of two or more numbers, first find the prime factors of the given numbers. Then find the product of all prime factors common to all the given numbers which are raised to the lowest power. The product of common prime factors with the lowest power gives HCF.
Example- Find the HCF of 20 and 30.
Solution:- Prime factors of 20 = 2 × 2 × 5 = 22 × 51
Prime factors of 30 = 2 × 3 × 5 = 21 × 31 × 51
∴ HCF = 21 × 51
Division Method :-
To find HCF by division method, divide the larger number by the smaller number, then divide the divisor by the remainder. Repeat this process till the remainder becomes zero. The last divisor obtained in this process is the HCF.
Example- Find the HCF of 108 and 288.
Solution:- HCF of 108 and 288 = 36
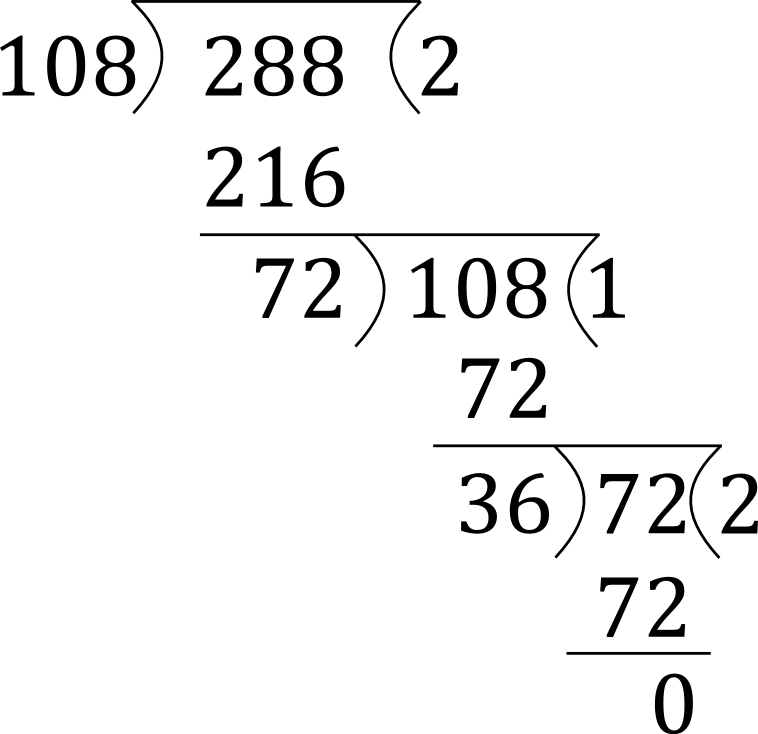
LCM of Fractions :-
To find the LCM of fractions, first reduced the fractions into lowest term. Then find the LCM of numerators and HCF of denominators.
| LCM of fractions = | |
| HCF of denominators |
| Example- Find the LCM of | , | , | and | ||||
| 3 | 5 | 7 | 13 |
LCM of 2, 3, 4 and 9 = 36
Here, denominators = 3, 5, 7 and 13
HCF of denominators = 1
| ∴ LCM of fractions = | and | = 36 | ||
| HCF of denominators | 1 |
HCF of Fractions :-
To find the HCF of fractions, first reduced the fraction into lowest term. Then find the HCF of numerators and LCM of denominators.
| HCF of fractions = | |
| LCM of denominators |
| Example- Find the HCF of | , | and | |||
| 2 | 4 | 5 |
HCF of numerators = HCF of 1, 3 and 4 = 1
Here, denominators = 2, 4 and 5
LCM of denominators = LCM of 2, 4 and 5 = 20
| ∴ HCF of fractions = | = | |||
| LCM of denominators | 20 |
Formula
| First number × Second number = LCM × HCF Product of two numbers = LCM of numbers × HCF of numbers |
| First Number = | |
| Second number |
| Second Number = | |
| First number |
| LCM of Numbers = | |
| HCF of numbers |
| HCF of Numbers = | |
| LCM of numbers |
Example- The LCM of two numbers is 72 and their HCF is 12. If the first number is 24, then find the second number.
Solution:- given, LCM = 72, HCF = 12, First number = 24
Let the second number be x.
Product of two numbers = LCM of numbers × HCF of numbers
⇒ 24 × x = 72 × 12
| x = 72 × | = 72 × | = 36 | ||
| 24 | 2 |
Example- Two numbers are in the ratio is 5 : 6 and their LCM is 480, then find the HCF of the numbers.
Solution:- Let the numbers be 5k and 6k.
∴ LCM = 480
5k × 6k = 480
⇒ 30k2 = 480
⇒ k2 = 480 ÷ 30
⇒ k2 = 16 ⇒ k = 4
∴ HCF = 16
Example- The product of two numbers is 1500 and their HCF is 10. Find the LCM of the numbers.
Solution:- Given, Product of numbers = 1500 , HCF = 10
| LCM of Numbers = | = | |||
| HCF of numbers | 10 |